Từ A ngoài (O) vẽ 2 tiếp tuyến  AB, AC (B,C là tiếp điểm) . AO cắt BC

Lời giải của Tự Học 365

Giải chi tiết:

1) Từ A ngoài (O) vẽ 2 tiếp tuyến  AB,AC (B,C là tiếp điểm ) . AO cắt BC tại H. Đường tròn đường kính CH cắt (O) tại điểm thứ 2 là D. Gọi T là trung điểm BD

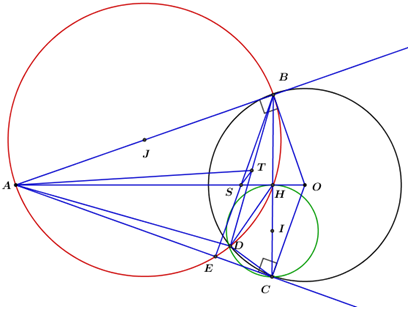
a) Chứng minh ABHD nội tiếp

Gọi \(I,\;J\) lần lượt là tâm của các đường tròn đường kính \(CH,\;AB.\)

Xét \(\left( J \right)\) ta có: \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn

\( \Rightarrow \angle ADB = {90^0}\)

Ta có: \(AB,\;AC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) tại các tiếp điểm \(B,\;C\) cắt nhau tại \(A\)

Và \(AO \cap BC = \left\{ H \right\} \Rightarrow AO \bot BC = \left\{ H \right\}\;\;hay\;\;\angle AHB = {90^0}\)  (tính chất hai tiếp tuyến cắt nhau)

Xét tứ giác \(ABHD\) ta có:

\(\angle ADB = \angle AHB = {90^0}\;\;\left( {cmt} \right)\)

\( \Rightarrow ABHD\) là tứ giác nội tiếp (dhnb).

b) Gọi E là giao điểm thứ 2 của đường tròn đường kính AB với AC. S là giao của AO với BE. Chứng minh TS//HD

Vì tứ giác \(ABHD\) là tứ giác nội tiếp (cmt)

\( \Rightarrow \angle DBH = \angle DAH\) (hai góc nội tiếp cùng chắn cung DH)

Xét đường tròn \(\left( I \right)\) ta có: \(\angle HDC\) là góc nội tiếp chắn nửa đường tròn

\(\begin{array}{l} \Rightarrow \angle HDC = {90^0}\\ \Rightarrow \angle BDA = \angle HCD = {90^0}.\end{array}\)

Lại có: \(\left\{ \begin{array}{l}\angle ADH = \angle ADB + \angle BDH = {90^0} + \angle BDH\\\angle BDC = \angle BDH + \angle HDC = {90^0} + \angle BDH\end{array} \right.\)

\( \Rightarrow \angle ADH = \angle BDC\;\left( { = {{90}^0} + \angle BDH} \right).\)

Xét \(\Delta ADH\) và \(\Delta BDC\) ta có:

\(\begin{array}{l}\angle HAD = \angle DAC\;\;\left( {cmt} \right)\\\angle ADH = \angle BDC\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ADH \sim \Delta BDC\;\;\left( {g - g} \right)\end{array}\)

\( \Rightarrow \frac{{AD}}{{BD}} = \frac{{AH}}{{BC}}\)  (các cặp cạnh tương ứng)

\( \Rightarrow \frac{{AD}}{{AH}} = \frac{{BD}}{{BC}} = \frac{{2TD}}{{2HC}} = \frac{{TD}}{{HC}}\) (T  là trung điểm của \(BD\)).

Xét \(\Delta TAD\) và \(\Delta CAH\) ta có:

\(\begin{array}{l}\frac{{AD}}{{AH}} = \frac{{TD}}{{CH}}\;\;\left( {cmt} \right)\\\angle TDA = \angle CHA = {90^0}\\ \Rightarrow \Delta TAD \sim \Delta CAH\;\;\left( {c - g - c} \right).\end{array}\)

\( \Rightarrow \angle TAD = \angle HAC\)  (hai góc tương ứng).

Mà: \(\left\{ \begin{array}{l}\angle TAD = \angle TAS + \angle HAD\\\angle HAC = \angle HAD + \angle DAE\end{array} \right. \Rightarrow \angle TAS = \angle DAE.\)

Mặt khác: \(\angle DAE = \angle DBE\) (hai góc nội tiếp cùng chắn cung DE)

\( \Rightarrow \angle TAS = \angle SBT\;\;\left( { = \angle EAD} \right)\)

\( \Rightarrow ABTS\) là tứ giác nội tiếp (dhnb).

\( \Rightarrow \angle STD = \angle BAS\)  (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)

Mà \(\angle BAS = \angle BDH\) (hai góc nội tiếp cùng chắn cung BH trong đường tròn (J))

\( \Rightarrow \angle STD = \angle TDH\;\left( { = \angle BAH} \right)\)

Lại có hai góc này ở vị trí so le trong

\( \Rightarrow ST//HD\;\;\left( {dpcm} \right).\)

2) Cho \(({O_1}),({O_2})\) cắt nhau tại 2 điểm A,b. Gọi MN là tiếp tuyến chung của 2 đường tròn với M,N lần lượt thuộc \(({O_1})\),\(({O_2})\).Qua A kẻ đường thẳng d song song với MN cắt \(({O_1}),({O_2}),BM,BN\) lần lượt tại C, D, F, G. Gọi E là giao của CM và DN. Chứng minh \(EF = EG.\)

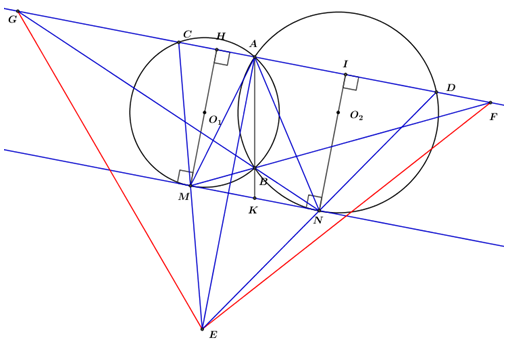
Gọi \(M{O_1} \cap d = \left\{ H \right\},\;\;N{O_2} \cap d = \left\{ I \right\},\;AB \cap MN = \left\{ K \right\}.\)

Ta có : \(MN//CD \Rightarrow \left\{ \begin{array}{l}{O_1}M \bot CD = \left\{ H \right\}\\{O_2}M \bot CD = \left\{ I \right\}\end{array} \right.\)

\( \Rightarrow {O_1}M,\;\;{O_2}N\) lần lượt là trung trực của \(CA\) và \(DA.\) (mối liên hệ giữa đường kính và dây cung)

\( \Rightarrow \left\{ \begin{array}{l}CH = HA,\;\;\angle MHA = {90^0}\\IA = ID,\;\;\angle NID = {90^0}\end{array} \right..\)

\( \Rightarrow MNIH\) là hình chữ nhật \(\left( {\angle M = \angle H = \angle I = {{90}^0}} \right).\)

\( \Rightarrow HI = MN = \frac{1}{2}CD.\)

Xét \(\Delta CED\) ta có: \(\left\{ \begin{array}{l}MN//CD\\MN = \frac{1}{2}CD\end{array} \right.\;\;\left( {cmt} \right)\)

\( \Rightarrow MN\) là đường trung bình của \(\Delta CED \Rightarrow M,\;N\) lần lượt là trung điểm của\(EC,\;\;ED.\)

\( \Rightarrow MC = ME,\;\;ND = NE.\)

Xét \(\Delta CAE\) ta có: \(M,\;H\) lần lượt là trung điểm của \(CA,\;CE\;\;\left( {cmt} \right)\)

\( \Rightarrow AM\) là đường trung bình của \(\Delta CAE\)  (định nghĩa).

\( \Rightarrow MH//AE\)  (định lý).

Mà \(MH \bot CD\;\;\left( {cmt} \right) \Rightarrow AE \bot CD\)  (từ vuông góc đến song song).

Xét \(\Delta MKA\) và \(\Delta BKM\) ta có:

\(\angle MAK = \angle KMB\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AB\))

\(MKA\;\;chung\)

\(\begin{array}{l} \Rightarrow \Delta MKA \sim \Delta BKM\;\;\left( {g - g} \right)\\ \Rightarrow \frac{{MK}}{{BK}} = \frac{{KA}}{{KM}} \Leftrightarrow K{M^2} = KA.BK.\;\;\;\;\left( 1 \right)\end{array}\)

Xét \(\Delta NKA\) và \(\Delta BKN\) ta có:

\(\angle NAK = \angle KNB\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AB\))

\(NKA\;\;chung\)

\(\begin{array}{l} \Rightarrow \Delta NKA \sim \Delta BKN\;\;\left( {g - g} \right)\\ \Rightarrow \frac{{NK}}{{BK}} = \frac{{KA}}{{KN}} \Leftrightarrow K{N^2} = KA.BK.\;\;\;\;\left( 2 \right)\end{array}\)

Từ (1) và (2) suy ra: \(KM = KN.\)

Do \(MN//FG,\) áp dụng định lý Ta-lét ta có:

\(\frac{{KN}}{{AG}} = \frac{{MK}}{{AF}} = \frac{{KB}}{{AB}} \Rightarrow AG = AF.\)

Mặt khác: \(AE \bot FG\;\;\left( {cmt} \right)\)

\( \Rightarrow EG = EF\;\) (tính chất đường trung trực).  (đpcm)