Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC có trung điểm của cạnh BC là điểm M( 3; - 1 ) đườ

Câu hỏi
Nhận biếtTrong mặt phẳng với hệ toạ độ \(Oxy,\) cho tam giác \(ABC\) có trung điểm của cạnh \(BC\) là điểm \(M\left( {3; - 1} \right)\), đường thẳng chứa đường cao kẻ từ đỉnh \(B\) đi qua điểm \(E\left( { - 1; - 3} \right)\) và đường thẳng chứa cạnh \(AC\) đi qua điểm \(F\left( {1;3} \right).\) Tìm toạ độ các đỉnh của tam giác \(ABC\) biết rằng điểm đối xứng của đỉnh \(A\) qua tâm đường tròn ngoại tiếp tam giác \(ABC\) là điểm \(D\left( {4; - 2} \right).\)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
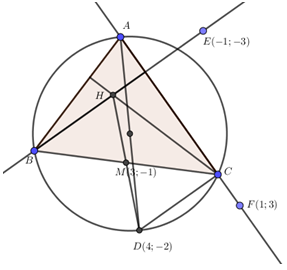
Gọi \(H\) là trực tâm của \(\Delta ABC,\) ta chứng minh được tứ giác \(BDCH\) là hình hành hành nên \(M\) là trung điểm \(HD\)
\( \Rightarrow H\left( {2;\,\,0} \right).\)
Đường thẳng \(BH\) có VTCP là \(\overrightarrow {EH} \left( {3;3} \right)\)
\( \Rightarrow VTPT{\rm{ }}{\overrightarrow n _{BH}} = \left( {1; - 1} \right) \Rightarrow BH:x - y - 2 = 0\)
+) \(AC \bot BH \Rightarrow \overrightarrow {{n_{AC}}} = \overrightarrow {{u_{BH}}} = \left( {1;1} \right) \Rightarrow AC:x + y - 4 = 0\)
+) \(AC \bot CD \Rightarrow \overrightarrow {{n_{DC}}} = \overrightarrow {{u_{AC}}} = \left( {1; - 1} \right) \Rightarrow DC:x - y - 6 = 0\)
+) \(C\) là giao điểm của \(AC\) và \(DC \Rightarrow \) toạ độ điểm \(C\) là nghiệm của hệ: \(\left\{ {\begin{array}{*{20}{c}}{x + y - 4 = 0}\\{x - y - 6 = 0}\end{array} \Rightarrow C\left( {5; - 1} \right)} \right.\)
+) \(M\) là trung điểm của \(BC \Rightarrow B\left( {1; - 1} \right),\,\,\,AH \bot BC \Rightarrow AH:x - 2 = 0.\)
+) \(A\) là giao điểm của \[AH,\,\,\,AC \Rightarrow \] toạ độ điểm \(A\) là nghiệm của hệ : \(\left\{ {\begin{array}{*{20}{c}}{x - 2 = 0}\\{x + y - 4 = 0}\end{array} \Rightarrow A\left( {2;2} \right)} \right.\)
Chọn A
