Trong mặt phẳng tọa độ Oxy cho parabol ( P ):,y = - 2x^2 và đường thẳng ( d ):,y = 2x - 4. a) Vẽ đ

Câu hỏi
Nhận biếtTrong mặt phẳng tọa độ Oxy cho parabol \(\left( P \right):\,\,y = - 2{x^2}\) và đường thẳng \(\left( d \right):\,\,y = 2x - 4\).
a) Vẽ đồ thị của (P) và (d) trên cùng mặt phẳng tọa độ.
b) Bằng phương pháp đại số, hãy tìm tọa độ giao điểm của (P) và (d)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Parabol \(\left( P \right):\,\,y = - 2{x^2}\)
Bảng giá trị:

Đường thẳng \(\left( d \right):\,\,y = 2x - 4\)
Cho \(x = 0 \Rightarrow y = - 4\)
Cho \(y = 0 \Rightarrow x = 2\)
Đồ thị như hình bên:
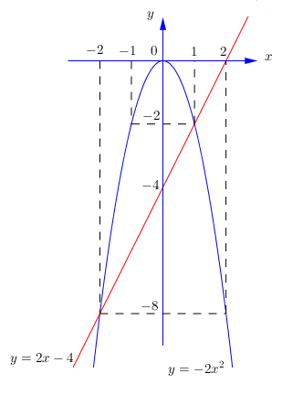
b) Xét phương trình hoành độ giao điểm \( - 2{x^2} = 2x - 4 \Leftrightarrow 2{x^2} + 2x - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = - 2\x = - 2 \Rightarrow y = - 8\end{array} \right.\)
Vậy giao điểm của (P) và (d) là các điểm có tọa độ \(\left( {1; - 2} \right);\,\,\left( { - 2; - 8} \right)\)
Chọn A

