Trên mặt phẳng tọa độ Oxy, cho điểm P( - 3; - 2 ) và đường tròn ( C )

Câu hỏi
Nhận biếtTrên mặt phẳng tọa độ \(Oxy, \) cho điểm \(P \left( { - 3; - 2} \right) \) và đường tròn \( \left( C \right):{ \left( {x - 3} \right)^2} + { \left( {y - 4} \right)^2} = 36 \). Từ điểm \(P \) kẻ các tiếp tuyến \(PM \) và \(PN \) tới đường tròn \( \left( C \right) \), với \(M \) và \(N \) là các tiếp điểm. Phương trình đường thẳng \(MN \) là:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
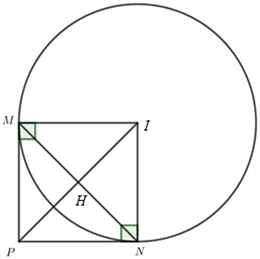
Đường tròn \(\left( C \right)\) có tâm \(I\left( {3;4} \right)\), bán kính \(R = IM = IN = 6\)
Ta có: \(\overrightarrow {IP} = \left( { - 6; - 6} \right) \Rightarrow IP = 6\sqrt 2 \)
Xét tam giác OMP vuông tại M (PM là tiếp tuyến của đường tròn \(\left( C \right)\) tại M)
\( \Rightarrow PM = \sqrt {I{P^2} - I{M^2}} = \sqrt {72 - 36} = 6\)
Tương tự ta cũng có \(PN = 6 \Rightarrow PN = PM = IM = IN = 6\)
Mà \(\angle IMP = {90^o}\) (PM là tiếp tuyến của đường tròn \(\left( C \right)\) tại M)
\( \Rightarrow \) IMPN là hình vuông
\( \Rightarrow \) MN nhận \(\overrightarrow {IP} = \left( { - 6; - 6} \right)\) làm VTPT và đi qua trung điểm \(H\left( {0;1} \right)\) của IP
\( \Rightarrow \) Phương trình \(MN: - 6\left( {x - 0} \right) - 6\left( {y - 1} \right) = 0 \Leftrightarrow x + y - 1 = 0\)
Chọn D.
