Trên hình vẽ là ba nửa đường tròn đường kính AB,,,AC,,,CB. Biết DC bot
Câu hỏi
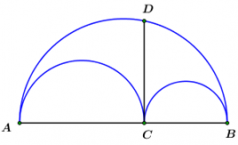
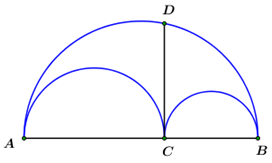
Nhận biếtTrên hình vẽ là ba nửa đường tròn đường kính \(AB,\,\,AC,\,\,CB.\) Biết \(DC \bot AB = \left\{ C \right\},\) khi đó tỉ số diện tích hình giới hạn bởi ba nửa đường tròn nói trên và diện tích hình tròn bán kính \(DC\) là:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
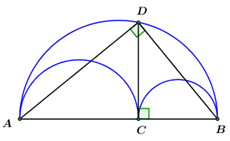
Xét đường tròn đường kính \(AB\) ta có: \(\angle ADB\) là góc nội tiếp chắn nửa đường tròn
\( \Rightarrow \angle ADB = {90^0}.\)
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(C{D^2} = AC.CB.\)
Diện tích hình tròn bán kính \(CD\) là: \({S_0} = \pi C{D^2} = \pi .AC.CB.\)
Diện tích nửa đường tròn đường kính \(AB\) là: \({S_1} = \frac{1}{2}.\pi .{\left( {\frac{{AB}}{2}} \right)^2} = \frac{{\pi A{B^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(AC\) là: \({S_2} = \frac{1}{2}.\pi .{\left( {\frac{{AC}}{2}} \right)^2} = \frac{{\pi A{C^2}}}{8}.\)
Diện tích nửa đường tròn đường kính \(BC\) là: \({S_3} = \frac{1}{2}.\pi .{\left( {\frac{{BC}}{2}} \right)^2} = \frac{{\pi B{C^2}}}{8}.\)
\( \Rightarrow \) Diện tích hình được giới hạn bởi ba đường tròn là:
\(S = {S_1} - {S_2} - {S_3} = \frac{{\pi A{B^2}}}{8} - \frac{{\pi A{C^2}}}{8} - \frac{{\pi B{C^2}}}{8} = \frac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right).\)
Lại có: \(AB = AC + BC \Rightarrow A{B^2} = A{C^2} + 2AC.BC + B{C^2}\)
\(\begin{array}{l} \Rightarrow S = \frac{\pi }{8}\left( {A{B^2} - A{C^2} - B{C^2}} \right) = \frac{\pi }{8}\left( {A{C^2} + B{C^2} + 2AC.BC - A{C^2} - B{C^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{\pi }{8}.2AC.BC = \frac{{\pi .AB.BC}}{4}.\\ \Rightarrow \frac{S}{{{S_0}}} = \frac{{\frac{{\pi .AB.BC}}{4}}}{{\pi .AC.BC}} = \frac{1}{4}.\end{array}\)
Chọn D.


