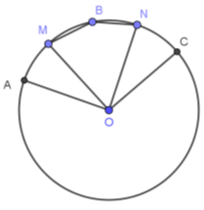
Trên đường tròn ( O;R ) lấy 3 điểm A,B,C sao cho AB = BC = R;M,N là cá

Câu hỏi
Nhận biếtTrên đường tròn \( \left( {O;R} \right) \) lấy \(3 \) điểm \(A,B,C \) sao cho \(AB = BC = R;M,N \) là các điểm nằm chính giữa của hai cung nhỏ \(AB \) và \(BC \) thì số đo góc \( \widehat {MBN} \) là
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
\(\Rightarrow \widehat {AOB} = {60^0}\).
Xét hai \(\Delta AOM\) và \(\Delta BOM\) có:
\(OA = OB\)
\(OM\) chung
\(AM = BM\)
\( \Rightarrow \Delta AOM = \Delta BOM\left( {c.c.c} \right)\)
\( \Rightarrow \widehat {AOM} = \widehat {MOB} = \frac{{\widehat {AOB}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\)
Tương tự ta có \(\widehat {NOB} = {30^0}\)
Vậy ta có \(\widehat {MON} = \widehat {MOB} + \widehat {NOB} = {30^0} + {30^0} = {60^0}\)
\( \Rightarrow \)sđ cung nhỏ \(MN\) là \({60^0} \Rightarrow \)sđ cung lớn \(MN\) là \({360^0} - {60^0} = {300^0}\)
\( \Rightarrow \widehat {MBN} = \frac{1}{2}{.300^0} = {150^0}\)(góc nội tiếp chắn cung lớn \(MN\))
Chọn B