. Trên cung nhỏ BC lấy một điểm M( M ne B,M ne C ), kẻ MI vuông góc AB

Câu hỏi
Nhận biếtTừ một điểm \(A\) nằm ngoài đường tròn tâm \(O,\) ta kẻ hai tiếp tuyến \(AB,\,\,AC\) với đường tròn (\(B,\,\,C\) là các tiếp điểm). Trên cung nhỏ \(BC\) lấy một điểm \(M\left( {M \ne B,\,\,M \ne C} \right),\) kẻ \(MI \bot AB,\,\,MK \bot AC\,\,\left( {I \in AB,\,\,K \in AC} \right).\)
a) Chứng minh \(AIMK\) là tứ giác nội tiếp đường tròn.
b) Kẻ \(MP \bot BC\,\,\left( {P \in BC} \right).\) Chứng minh rằng \(\angle MPK = \angle MBC.\)
c) Xác định vị trí của \(M\) trên cung nhỏ \(BC\) để tích \(MI.MK.MP\) đạt giá trị lớn nhất.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
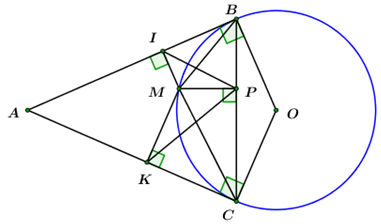
a) Chứng minh \(AIMK\) là tứ giác nội tiếp đường tròn.
Ta có: \(\left\{ \begin{array}{l}MI \bot AB = \left\{ I \right\} \Rightarrow \angle AIM = {90^0}\\MK \bot AC = \left\{ K \right\} \Rightarrow \angle AKM = {90^0}\end{array} \right.\)
\( \Rightarrow \angle AIM + \angle AKM = {90^0} + {90^0} = {180^0}\).
Mà hai góc này ở vị trí đối diện
\( \Rightarrow AIMK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\)). (đpcm)
b) Kẻ \(MP \bot BC\,\,\left( {P \in BC} \right).\) Chứng minh rằng \(\angle MPK = \angle MBC.\)
Ta có: \(MP \bot BC = \left\{ P \right\} \Rightarrow \angle MPC = {90^0}.\)
\( \Rightarrow \angle MKC + \angle MPC = {90^0} + {90^0} = {180^0}\)
Mà hai góc này ở vị trí đối diện
\( \Rightarrow MPCK\) là tứ giác nội tiếp (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
\( \Rightarrow \angle MPK = \angle MCK\) (hai góc nội tiếp cùng chắn cung \(MK\))
Xét đường tròn \(\left( O \right)\) ta có: \(\angle MBC = \angle MCK\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(MC\))
\( \Rightarrow \angle MBC = \angle MPK\,\,\left( { = \angle MCK} \right)\) (đpcm).
c) Xác định vị trí của \(M\) trên cung nhỏ \(BC\) để tích \(MI.MK.MP\) đạt giá trị lớn nhất.
Nối \(I\) với \(P\)
Xét tứ giác \(PBIM\) ta có :
\(\left. \begin{array}{l}\angle BPM = {90^0}\,\,\,\left( {MP \bot BC} \right)\\\angle BIM = {90^0}\,\,\,\left( {MI \bot BA} \right)\end{array} \right\} \Rightarrow \angle BPM + \angle BIM = {180^0}\)
Mà 2 góc này ở vị trí đối diện ⇒ tứ giác \(PBIM\) là tứ giác nội tiếp. (dhnb)
\( \Rightarrow \angle MIP = \angle MBP\) (2 góc nội tiếp cùng chắng cung \(MP\))
Mà \(\angle MBP = \angle MPK\,\,\,\left( {cmt} \right) \Rightarrow \angle MIP = \angle MPK\)
Ta có : \(\angle PMI + \angle PBI = {180^0};\angle PMK + \angle PCK = {180^0}\)
Mà \(\angle ABC = \angle ACB\) (tính chất hai tiếp tuyến cắt nhau)
Hay \(\angle IBP = \angle PCK \Rightarrow \angle PMK = \angle PMI.\)
Xét \(\Delta MIP\) và \(\Delta MPK\) có :
\(\left. \begin{array}{l}\angle PMK = \angle PMI\left( {cmt} \right)\\\angle MIP = \angle MPK\left( {cmt} \right)\end{array} \right\} \Rightarrow \Delta MIP \sim \Delta MPK\left( {g.g} \right)\)
\( \Rightarrow \frac{{MI}}{{MP}} = \frac{{MP}}{{MK}}\) (cạnh tương ứng) \( \Rightarrow MI.MK = M{P^2} \Rightarrow MI.MK.MP = M{P^3}\)
\( \Rightarrow MI.MK.MP\) lớn nhất khi \(MP\) lớn nhất.
Gọi \(P'\) là trung điểm của \(BC\) và \(M'\) là giao điểm của \(OP'\) với đường tròn (\(M'\) thuộc cung nhỏ \(BC\)).
Khi đó \(M'\) là điểm chính giữa của cung nhỏ \(BC\).
Dễ thấy \(MP \le M'P'\) không đổi nên \(MP\) lớn nhất khi \(M \equiv M'\) là điểm chính giữa của cung nhỏ \(BC\).

