Tính diện tích hình hoa thị bốn cánh (như hình vẽ), cạnh hình vuông bằ
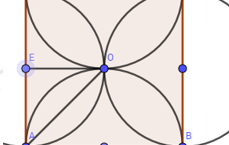
Câu hỏi
Nhận biếtTính diện tích hình hoa thị bốn cánh (như hình vẽ), cạnh hình vuông bằng \(2a\).
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: \({{S}_{AOE}}=\frac{1}{2}\text{AE}.OE=\frac{1}{2}{{a}^{2}}\)
Mặt khác: \({{S}_{qAOE}}=\frac{\pi {{\left( a \right)}^{2}}.90}{360}=\frac{\pi {{a}^{2}}}{4}\)
Suy ra diện tích hình viên phân giới hạn bởi cung \(\overset\frown{AO}\) và đoạn AO là:
\({{S}_{qAOE}}-{{S}_{AOE}}=\frac{\pi {{a}^{2}}}{4}-\frac{{{a}^{2}}}{2}=\frac{{{a}^{2}}}{4}\left( \pi -2 \right)\)
Hình hoa thị gồm 8 hình viên phân có diện tích bằng nhau. Vậy diện tích hình hoa thị bằng:
\(S=8\left( {{S}_{qAOE}}-{{S}_{AOE}} \right)=2{{a}^{2}}\left( \pi -2 \right)\)
Chọn D
