Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất
Câu hỏi
Nhận biếtTìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Kẻ BH ⊥ AC
SIBC = 1/2BH.IC = 1/2IB.IC.sin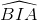
Do 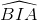= 1800 – 2
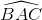không đổi nên SIBC lớn nhất khi IB.IC lớn nhất
IB.IC = IA.IC ≤ (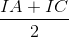
)2 = 
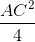≤ R2
Dấu “=” xảy ra ⇔ IA = IC và A đối xứng với C qua tâm O
