Tìm tất cả các số thực m để phương trình | x^2 - 2x | - m = 0 có bốn nghiệm phân biệt

Câu hỏi
Nhận biếtTìm tất cả các số thực m để phương trình \(\left| {{x^2} - 2x} \right| - m = 0\) có bốn nghiệm phân biệt
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
\(\left| {{x^2} - 2x} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 2x} \right| = m\) (1)
Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\) và đường thẳng \(y = m.\)
Khảo sát hàm số \(y = \left| {{x^2} - 2x} \right|\):
TXĐ: \(D = R\)
Vẽ đồ thị của hàm số \(y = \left| {{x^2} - 2x} \right|\) bằng cách giữ nguyên phần phía trên trục Ox và lấy đối xứng phần đồ thị phía dưới trục Ox của hàm số \(y = {x^2} - 2x\).
Xét hàm số \(y = {x^2} - 2x\) có đỉnh là \(I\left( {1; - 1} \right)\)
Ta có đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\):
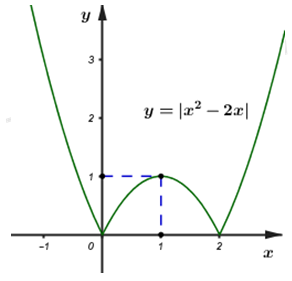
Dựa vào đồ thị hàm số ta có đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {{x^2} - 2x} \right|\) tại 4 điểm phân biệt \( \Leftrightarrow 0 < m < 1.\)
Chọn B.
