Tìm tất cả các số nguyên n để n4 + n3 + n2 là số chính phương.
Câu hỏi
Nhận biếtTìm tất cả các số nguyên n để n4 + n3 + n2 là số chính phương.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có : A = n4 + n3 + n2 = n2 (n2 + n + 1).
+) Với n = 0 thì A = 0 (thỏa mãn)
+) Với n ≠ 0 thì A là số chính phương khi và chỉ khi n2 + n + 1 là số chính phương. Khi đó n2 + n + 1 = k2 (k ϵ N)
<=> 4(n2 + n + 1) = 4k2
<=> (2n + 1)2 – 4k2 = -3 => (2n + 1 - 2k)(2n + 1 + 2k) = - 3
Vì 2n + 1 + 2k ≥ 2n + 1 - 2k với mọi giá trị của n ϵ Z, k ϵ N nên tương đương với 2 hệ phương trình sau:
(I)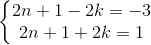 
=> n = -1 (thỏa mãn)
(II)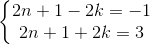 
=> n = 0 (loại)
Vậy n = 0 và n = -1
