Tìm tất cả các giá trị của m để phương trình | x + 1 | + | x - 1 | = m^2 - 2 có hai nghiệm phân biệt

Lời giải của Tự Học 365

Giải chi tiết:

Hướng dẫn giải chi tiết

Ta có \(y = \left| {x + 1} \right| + \left| {x - 1} \right| = \left\{ \matrix{   - 2x\,\,\,\left( {x <  - 1} \right) \hfill \cr   2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right) \hfill \cr   2x\,\,\,\,\left( {x \ge 1} \right) \hfill \cr}  \right.\) và có đồ thi như sau:

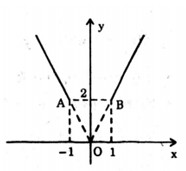
Đường thẳng \(d:\,\,y = {m^2} - 2\) song song với trục hoành.

Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = \left\{ \matrix{   - 2x\,\,\,\left( {x <  - 1} \right) \hfill \cr   2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right) \hfill \cr   2x\,\,\,\,\left( {x \ge 1} \right) \hfill \cr}  \right.\) và đường thẳng \(d:\,\,y = {m^2} - 2\).

Nhìn vào đồ thị ta thấy phương trình đã cho có hai nghiệm phân biệt khi \({m^2} - 2 > 2 \Rightarrow {m^2} > 4 \Leftrightarrow \left[ \matrix{  m <  - 2 \hfill \cr   m > 2 \hfill \cr}  \right.\).

Chọn C.