Tìm tất cả các giá trị của m để phương trình có hai nghiệm x1 x2 khác 0 và thỏa điều kiện <
Câu hỏi
Nhận biếtTìm tất cả các giá trị của m để phương trình có hai nghiệm x1, x2 khác 0 và thỏa điều kiện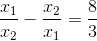 
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Với x1, x2 ≠ 0, ta có : 
<=> 
<=> 3(x1 + x2)(x1 – x2) = 8x1x2
Ta có : a.c = -3m2 ≤ 0 nên ∆ ≥ 0, với mọi m.
Khi ∆ ≥ 0 ta có : x1 + x2 = 
và x1.x2 = 
≤ 0
Điều kiện để phương trình có 2 nghiệm khác 0 mà m ≠ 0 => ∆ > 0 và x1.x2 < 0
=> x1 < x2
Với a = 1 => x1 = 
và x2 = 
=> x1 – x2 = 2
= 
Do đó, ycbt <=> 
và m ≠ 0
<=> 
(hiển nhiên m = 0 không là nghiệm)
<=> 4m4 – 3m2 – 1 = 0 <=> m2 = 1 hay m2 = -1/4 (loại) <=> m = ±1
Luyện tập
Câu hỏi liên quan
Diện tích mặt cầu có bán kính bằng 2 cm là:
Phương trình 3x2 – 5x – 2015 có tổng hai nghiệm là:
Phương trình nào sau đây có đúng hai nghiệm phân biệt:
Hàm số nào đồng biến trên R:
Cho đường tròn (O; 25 cm) và dây AB = 40 cm. Khi đó khoảng cách từ tâm O đến dây AB là:
(1 điểm) Giải phương trình: 2x2 + x – 15 = 0