Tìm m để (d) cắt (P) tại hai điểm phân biệt có tọa độ (x1; y1) và (x2;

Câu hỏi
Nhận biếtTìm m để (d) cắt (P) tại hai điểm phân biệt có tọa độ (x1; y1) và (x2; y2) sao cho x1x2 (y1 + y2) + 48 = 0
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình 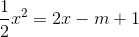
<=> 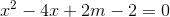 (1)
(1)
Để (d) cắt (P) tại hai điểm phân biệt nên (1) có hai nghiệm phân biệt
<=> ∆’ > 0 <=> 6 - 2m > 0 <=> m < 3
Vì (x1; y1) và (x2; y2) là tọa độ giao điểm của (d) và (P) nên x1; x2 là nghiệm của phương trình (1) và y1 = 2x1 – m +1 , y2 = 2x2 – m + 1
Theo hệ thức Vi-et ta có x1 + x2 = 4 ; x1x2 = 2m – 2 . Thay y1, y2 vào :
x1x2 (y1 + y2) + 48 = 0 có x1x2 (2x1 + 2x2 – 2m + 2) + 48 = 0
=> (2m - 2)(10 - 2m) + 48 = 0
<=> m2 – 6m – 7 = 0 <=> m = -1 (thảo mãn m < 3) hoặc m = 7 (không thỏa mãn m < 3)
Vậy m = -1 .

