Tìm các giá trị của m để phương trình (1) có hai nghiệm x1 x2 thỏa mãn: x1x2.( x1x2 – 2 ) = 3(

Câu hỏi
Nhận biếtTìm các giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn:
x1x2.( x1x2 – 2 ) = 3( x1 + x2 ).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: ∆ = 1 – 4(1 + m) = -3 – 4m.
Để phương trình có nghiệm thì ∆ ≥ 0 <=> - 3 – 4m ≥ 0
<=> 4m ≤ -3 <=> m ≤ 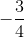 (1).
(1).
Theo hệ thức Vi-ét ta có: x1 + x2 = 1 và x1.x2 = 1 + m
Thay vào đẳng thức: x1x2.( x1x2 – 2 ) = 3( x1 + x2 ), ta được:
(1 + m)(1 + m – 2) = 3 <=> m2 = 4 <=> m = ± 2.
Đối chiếu với điều kiện (1) suy ra chỉ có m = -2 thỏa mãn.

