Tia phân giác góc góc BAD của hình bình hành ABCD cắt các đường thẳng BC và DC lần lượt tại hai

Câu hỏi
Nhận biếtTia phân giác góc \(\widehat {BAD}\) của hình bình hành ABCD cắt các đường thẳng BC và DC lần lượt tại hai điểm N và M Dựng ra phía ngoài hình bình hành ABCD tam giác cân MCO với \(\widehat {MOC} = \widehat {BAD}\) . Khi đó:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có BM//AD nên \(\widehat {BMA} = \widehat {MAD}.\)Mặt khác AM là phân giác của \(\widehat {BAD}\) nên \(\widehat {BAM} = \widehat {MAD}.\)
Từ đó \(\widehat {BAM} = \widehat {AMB.}\)
Vậy \(\Delta ABM\) cân tại B Suy ra \(BM = BA = DC.\)
Tam giác OCM cân tại O nên OM = OC Đặt \(\alpha = \widehat {BAD},\) ta có \(\widehat {OCD} = \widehat {BCD} + \widehat {OCM} = \alpha + {1 \over 2}\left( {{{180}^0} - \alpha } \right) = {90^0} + {\alpha \over 2}\,\,\left( 1 \right).\)
Các góc \(\widehat {BMO},\,\widehat {OMC}\) kề bù nên
\(\widehat {BMO} = {180^0} - \,\widehat {OMC} = {180^0} - \,\widehat {OCM} = {90^0} + {\alpha \over 2}\,\,\left( 2 \right).\)
Từ (1) và (2) suy ra \(\widehat {OCD} = \widehat {BMO}.\)
Xét hai tam giác \(\Delta OBM,\,\Delta ODC\) có \(\left\{ \matrix{\widehat {OCD} = \widehat {BMO} \hfill \cr OM = OC \hfill \cr BM = CD \hfill \cr} \right.\) nên \(\Delta OBM = \Delta ODC\,\,\left( {c.g.c} \right).\)
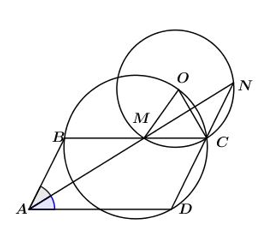
Do đó \(\widehat {OBM} = \widehat {ODC}.\) Điều này chứng tỏ BOCD là tứ giác nội tiếp. Do đó bốn điểm B, O, C, D thuộc cùng một đường tròn.Chọn đáp án A.

