Tam giác ABC có A( - 3; - 2);B(5;2) và trực tâm H(5;0). Tìm tọa độ đỉnh C.

Câu hỏi
Nhận biếtTam giác ABC có \(A( - 3; - 2),\;B(5;2)\) và trực tâm \(H(5;0)\). Tìm tọa độ đỉnh C.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
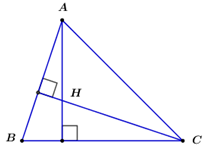
Gọi \(C\left( {{x_0};{y_0}} \right)\) là điểm cần tìm.
Ta có : \(\overrightarrow {AH} = \left( {8;2} \right)\,\,;\,\,\overrightarrow {BC} = \left( {{x_0} - 5;{y_0} - 2} \right)\)
\(\overrightarrow {AB} = \left( {8;4} \right)\,\,;\,\,\overrightarrow {CH} = \left( {5 - {x_0}; - {y_0}} \right)\)
H là trực tâm tam giác ABC \( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} \bot \overrightarrow {BC} \\\overrightarrow {CH} \bot \overrightarrow {AB} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8\left( {{x_0} - 5} \right) + 2\left( {{y_0} - 2} \right) = 0\\8\left( {5 - {x_0}} \right) + 4\left( { - {y_0}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}8{x_0} + 2{y_0} = 44\\ - 8{x_0} - 4{y_0} = - 40\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 6\\{y_0} = - 2\end{array} \right.\)
Chọn A.
