Tam giác ABC cân tại B có angle ABC = 120^0AB = 12cm và nội tiếp đường tròn ( O ). Bán kính của đườn

Câu hỏi
Nhận biếtTam giác \(ABC\) cân tại \(B\) có \(\angle ABC = {120^0},\,\,AB = 12cm\) và nội tiếp đường tròn \(\left( O \right).\) Bán kính của đường tròn \(\left( O \right)\) bằng:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
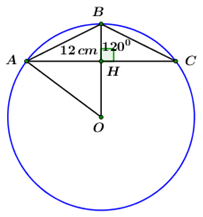
Gọi \(H\) là trung điểm của \(AC.\)
Ta có \(\Delta ABC\) cân tại \(B \Rightarrow BH \bot AC \Rightarrow OB \bot AC = \left\{ H \right\}.\)
\( \Rightarrow BO\) là đường phân giác của \(\angle ABC \Rightarrow \angle ABO = {60^0}\)
Lại có \(\Delta ABO\) cân tại \(O\,\,\,\left( {OB = OA = R} \right)\)
\( \Rightarrow \Delta ABO\) là tam giác đều (tính chất).
\( \Rightarrow AB = AO = BO = 12cm.\)
Chọn B.

