Người ta gắn một hình nón có bán kính đáy R = 8cm, độ dài đường cao h
Câu hỏi
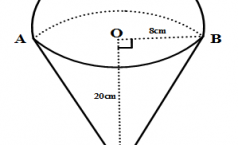
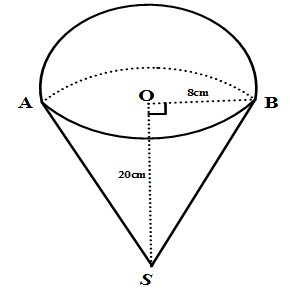
Nhận biếtNgười ta gắn một hình nón có bán kính đáy R = 8cm, độ dài đường cao h = 20 cm vào một nửa hình cầu có bán kính bằng bán kính hình nón (theo hình bên). Giá trị gần đúng thể tích của hình tạo thành (kết quả làm tròn đến chữ số thập phân thứ nhất) là :
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Thể tích của một nửa hình cầu là:
\({{V}_{1}}=\frac{1}{2}.\frac{4}{3}\pi {{R}^{3}}=\frac{2}{3}\pi {{.8}^{3}}=\frac{1024}{3}\pi \left( c{{m}^{3}} \right)\)
Thể tích của hình nón là:
\({{V}_{2}}=\frac{1}{3}Sh=\frac{1}{3}.\pi {{R}^{2}}.h=\frac{1}{3}\pi {{.8}^{2}}.20=\frac{1280}{3}\pi \left( c{{m}^{3}} \right)\)
Thể tích của hình tạo thành là:
\(V={{V}_{1}}+{{V}_{2}}=\frac{1024}{3}\pi +\frac{1280}{3}\pi =768\pi =2413\left( c{{m}^{3}} \right)\)
Chọn A

