Một cô gái cao 165cm, mắt cách đỉnh đầu 10cm đứng gần chiếc
Câu hỏi
Nhận biết(1,5 điểm)
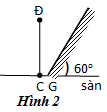
Một cô gái cao 165cm, mắt cách đỉnh đầu 10cm đứng gần chiếc gương lớn G đặt nghiêng 600 so với mặt sàn nằm ngang (Hình 2 với C là chân, Đ là đỉnh đầu).

1. Tìm khoảng cách xa nhất từ chân cô gái tới vị trí đặt gương để cô ấy ngắm được toàn thân mình qua gương. Tìm kích thước tối thiểu của gương khi đó.
2. Khi cô gái từ từ lùi xa gương thì hình ảnh cô ấy dịch chuyển thế nào?
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1. Để nhìn thấy toàn thân ở khoảng cách xa nhất phải thỏa mãn hình vẽ:
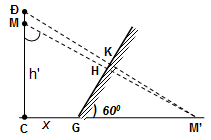
* Dễ thấy M’ đối xứng M qua gương tạo ra ∆MCM’ vuông ở C có góc 600 nên: MC = MH = M’H = h’ = 155cm
suy ra: \(GM' = {{h'} \over {c{\rm{os}}{{30}^0}}} = {{2h'} \over {\sqrt 3 }}\)
x = CM’ - GM’= \(2h'.c{\rm{os}}{30^0} - {{2h'} \over {\sqrt 3 }} = {{h'} \over {\sqrt 3 }} \approx 89,49cm\)
* Có: tan(ĐM’C) = \({{165} \over {155\sqrt 3 }}\) nên <(ĐM’C) = 31,570
Tìm được: HK = HM’.tan(HM’K)= 4,25cm
Suy ra : GK = GH + HK = M’H.tan 300 +4,25 = 93,74cm
2. Hình ảnh quan sát được lùi xa và đi xuống, mất dần từ chân đến đầu









