Một hình viên phân có số đo cung 90^0 diện tích 2pi -4. Tính độ dài dây của hình viên phân.

Câu hỏi
Nhận biếtMột hình viên phân có số đo cung \({{90}^{0}}\), diện tích \(2\pi -4\). Tính độ dài dây của hình viên phân.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
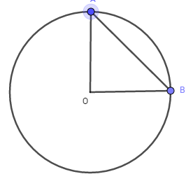
Giả sử hình viên phân giới hạn bởi cung \(\overset\frown{AB}\) và dây \(AB\). Ta có \(S={{S}_{qOAB}}-{{S}_{\Delta OAB}}\)
Theo giả thiết hình viên phân có số đo cung \({{90}^{0}}\) nên ta có \(\left\{ \begin{align} & {{S}_{\Delta OAB}}=\frac{1}{2}OA.OB=\frac{1}{2}{{R}^{2}} \\ & {{S}_{qOAB}}=\frac{\pi {{R}^{2}}.90}{360}=\frac{\pi {{R}^{2}}}{4} \\ \end{align} \right.\)
Suy ra ta có phương trình cũng có
\(\begin{align} & \frac{\pi {{R}^{2}}}{4}-\frac{1}{2}{{R}^{2}}=2\pi -4 \\ & \Leftrightarrow {{R}^{2}}\left( \frac{\pi }{4}-\frac{1}{2} \right)=2\pi -4 \\ & \Leftrightarrow {{R}^{2}}\left( \frac{2\pi -4}{8} \right)=2\pi -4 \\ & \Leftrightarrow {{R}^{2}}=8\Leftrightarrow R=2\sqrt{2} \\ \end{align}\)
Áp dụng định lý Pitago ta có: \(A{{B}^{2}}=O{{A}^{2}}+O{{B}^{2}}=2{{R}^{2}}=16\Rightarrow AB=4\)
Chọn D

