Một hình thang cân có đường chéo vuông góc với cạnh bên. Biết rằng đáy

Câu hỏi
Nhận biếtMột hình thang cân có đường chéo vuông góc với cạnh bên. Biết rằng đáy nhỏ dài \(14cm, \) đáy lớn dài \(50cm. \) Tính diện tích và chu vi hình thang.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
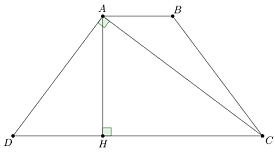
Ta có: \(\angle DAC = \angle DBC = {90^0}\,\,\left( {gt} \right)\) nên \(ABCD\) là tứ giác nội tiếp.
\( \Rightarrow \angle BAD + \angle BCD = {180^0}\).
Mà \(\angle BAD + \angle ADC = {180^0}\) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \angle ADC = \angle BCD\).
\( \Rightarrow ABCD\) là hình thang cân.
Kẻ \(AH \bot CD\) tại \(H.\)
Ta có:
\(\begin{array}{l}HD = \dfrac{{CD - AB}}{2} = 18\,\,\,\left( {cm} \right)\\HC = CD - HD = 32\,\,\,\left( {cm} \right).\end{array}\)
Xét tam giác \(ACD\) vuông tại \(A,\) đường cao \(AH,\) ta có:
\(A{H^2} = HC.HD = 18.32 \Rightarrow AH = 24\,\,\,\,\left( {cm} \right).\)
Diện tích hình thang \(ABCD\) là: \({S_{ABCD}} = \dfrac{1}{2}AH.\left( {AB + CD} \right) = \dfrac{1}{2}.24.\left( {14 + 50} \right) = 768\,\,\,\left( {c{m^2}} \right).\)
Áp dụng định lý Pytago trong tam giác \(AHD\) vuông tại \(H:\)
\(A{D^2} = A{H^2} + H{D^2} = {24^2} + {18^2} = 900 \Rightarrow AD = 30\,\,\,\left( {cm} \right).\)
Do \(ABCD\) là hình thang cân nên \(BC = AD = 30\,\,\left( {cm} \right).\)
Chu vi hình thang \(ABCD\) là: \({C_{ABCD}} = AB + BC + CD + AD = 14 + 30 + 50 + 30 = 124\,\,\,\left( {cm} \right).\)
Vậy \({S_{ABCD}} = 768\,\,c{m^2},\,\,{C_{ABCD}} = 124\,\,cm.\).
Chọn D.

