Một đường thẳng d thay đổi luôn đi qua A cắt (O) và (O') thứ tự tại M
Câu hỏi
Nhận biếtMột đường thẳng d thay đổi luôn đi qua A cắt (O) và (O') thứ tự tại M và N. Xác định vị trí của d để CM + DN đạt giá trị lớn nhất.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Ta có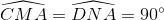 
(góc nội tiếp chắn nửa đường tròn); suy ra CM // DN hay CMND là hình thang.
Gọi I, K thứ tự là trung điểm của MN và CD. Khi đó IK là đường trung bình của hình thang CMND. Suy ra IK // CM // DN (1) và CM + DN = 2.IK (2)
Từ (1) suy ra IK ┴ MN => IK ≤ KA (3) (KA là hằng số do A và K cố định).
Từ (2) và (3) suy ra: CM + DN ≤ 2KA. Dấu “ = ” xảy ra khi và chỉ khi IK = AK <=> d ┴ AK tại A.
Vậy khi đường thẳng d vuông góc AK tại A thì (CM + DN) đạt giá trị lớn nhất bằng 2KA.
