Một công ty muốn xây dựng một đường ống dẫn dầu từ điểm A trên bờ biển
Câu hỏi
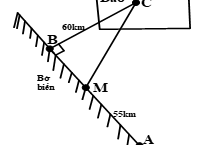
Nhận biếtMột công ty muốn xây dựng một đường ống dẫn dầu từ điểm A trên bờ biển đến một điểm C trên một hòn đảo như hình vẽ. Giá để xây dựng đường ống trên bờ là 40 000 USD mỗi km và 130 000 USD mỗi km để xây dưới nước. Hỏi công ty nên xây đường ống theo phương án nào để tiết kiệm chi phí nhất? Biết rằng công ty đưa ra ba phương án:
Phương án 1: Xây đường ống từ điểm A trên bờ đến điểm C trên đảo.
Phương án 2: Xây đường ống từ điểm A đến điểm M trên bờ biển, rồi xây đường ống từ điểm M đến điểm C trên hòn đảo.
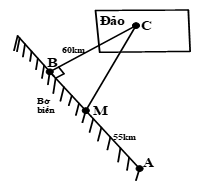
Phương án 3: Xây đường ống từ điểm A đến điểm B trên bờ biển, rồi xây đường ống từ điểm B đến điểm C trên hòn đảo. Biết: BC = 60km, AB = 100km, AM = 55km
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Độ dài đoạn BM: \(BM=AB-AM=100-55=45km\) Xét tam giác MBC vuông tại B, áp dụng định lý Pytago, ta có:
\(CM=\sqrt{B{{C}^{2}}+B{{M}^{2}}}=\sqrt{{{60}^{2}}+{{45}^{2}}}=\sqrt{5625}=75km\)
Xét tam giác ABC vuông tại B, áp dụng định lý Pytago, ta có:
\(AC=\sqrt{B{{C}^{2}}+A{{B}^{2}}}=\sqrt{{{60}^{2}}+{{100}^{2}}}=\sqrt{13600}\approx 116,62km\)
Tổng số tiền xây dựng theo phương án 1:
\({{T}_{1}}={{130}^{{}}}000.116,62=15160474,93\)(USD)
Tổng số tiền xây dựng theo phương án 2:
\({{T}_{2}}={{40}^{{}}}000.55+{{130}^{{}}}000.75=11950000\) (USD)
Tổng số tiền xây dựng theo phương án 3:
\({{T}_{3}}={{40}^{{}}}000.100+{{130}^{{}}}000.60=11800000\) (USD)
Do \({{T}_{1}}>{{T}_{2}}>{{T}_{3}}\) nên phương án 3 là phương án xây dựng đường ống mà tiết kiệm chi phí nhất.
Chú ý:
Bình luận về bài toán:
Đây là dạng toán tương đối hay. Vừa yêu cầu các em phải biết sử dụng kiến thức hình học (định lýPitago), vừa yêu cầu các em phải biết tính toán chi phí để tìm ra phương án tối ưu (tức là phương án sử dụng chi phí ít nhất). Các em cần đọc kỹ đề để xem chi phí cho từng phương án như thế nào, tránh bị nhầm lẫn khi tính chi phí các phương án. (phương án dưới nước chi phí bao nhiêu, phương án trên bờ chi phí bao nhiêu?)
