Một chiếc máy bay bay lên với vận tốc 500km/h. Đường bay lên tạo với

Câu hỏi
Nhận biết1) Một chiếc máy bay bay lên với vận tốc \(500km/h.\) Đường bay lên tạo với phương nằm ngang một góc \(30^\circ .\) Hỏi sau \(6\) phút kể từ lúc cất cánh, máy bay lên cao được bao nhiêu ki-lô-mét theo phương thẳng đứng?
2) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(AB.\) Vẽ hai tiếp tuyến \(Ax,\,By\) với nửa đường tròn đó. Trên tia \(Ax\) lấy điểm \(M\) sao cho \(AM > R.\) Từ \(M\) kẻ tiếp tuyến \(MC\) với nửa đường tròn \(\left( O \right)\) (\(C\) là tiếp điểm). Tia \(MC\) cắt tia \(By\) tại \(D.\)
a) Chứng minh \(MD = MA + BD\) và \(\Delta OMD\) vuông.
b) Cho \(AM = 2R.\) Tính \(BD\) và chu vi tứ giác \(ABDM.\)
c) Tia \(AC\) cắt tia \(By\) tại \(K.\) Chứng minh \(OK \bot BM.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Một chiếc máy bay bay lên với vận tốc \(500km/h.\) Đường bay lên tạo với phương nằm ngang một góc \(30^\circ .\) Hỏi sau \(6\) phút kể từ lúc cất cánh, máy bay lên cao được bao nhiêu ki-lô-mét theo phương thẳng đứng?
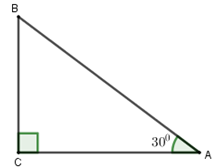
\(6\) phút \( = 0,1\) giờ.
Gọi \(AB\) là đoạn đường máy bay bay lên trong \(6\) phút thì \(BC\) chính là độ cao máy bay đạt được sau \(6\) phút.
Sau \(6\) phút máy bay bay được quãng đường là \(AB = 500.0,1 = 50km.\)
Độ cao của máy bay là \(BC = 50.\sin A = 50.\sin 30^\circ = 25km.\)
2) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(AB.\) Vẽ hai tiếp tuyến \(Ax,\,By\) với nửa đường tròn đó. Trên tia \(Ax\) lấy điểm \(M\) sao cho \(AM > R.\) Từ \(M\) kẻ tiếp tuyến \(MC\) với nửa đường tròn \(\left( O \right)\) (\(C\) là tiếp điểm). Tia \(MC\) cắt tia \(By\) tại \(D.\)
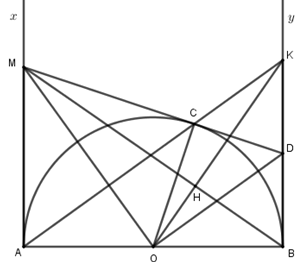
a) Chứng minh \(MD = MA + BD\) và \(\Delta OMD\) vuông.
Xét \(\left( O \right):\) \(MA,\,MC\) là \(2\) tiếp tuyến cắt nhau tại \(M\) với tiếp điểm \(A\) và \(C\) \( \Rightarrow MA = MC.\)
\(DC,\,DB\) là \(2\) tiếp tuyến cắt nhau tại \(D\) với tiếp điểm \(B\) và \(C\) \( \Rightarrow DB = DC\)
Mà \(MD = MC + CD\)
\( \Rightarrow MD = MA + DB\)
Xét \(\left( O \right):\)
\(MA,\,MC\) là \(2\) tiếp tuyến cắt nhau tại \(M\) với tiếp điểm \(A\) và \(C\) \( \Rightarrow OM\) là tia phân giác của \(\widehat {AOC}\)
\(DC,\,DB\) là \(2\) tiếp tuyến cắt nhau tại \(D\) với tiếp điểm \(B\) và \(C\) \( \Rightarrow OD\) là tia phân giác của \(\widehat {COB}\)
Mà \(\widehat {AOC}\) và \(\widehat {COB}\) là hai góc kề bù
\( \Rightarrow OM \bot OD\) tại \(D\)
\( \Rightarrow \widehat {MOD} = 90^\circ \) nên \(\Delta OMD\) vuông tại \(O.\)
b) Cho \(AM = 2R.\) Tính \(BD\) và chu vi tứ giác \(ABDM.\)
\(AM = 2R \Rightarrow MC = 2R\)
Xét tam giác \(MOD\) vuông tại \(O,\) đường cao \(OC,\) có :
\(MC.DC = O{M^2}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow 2R.CD = {R^2} \Rightarrow CD = \frac{R}{2}\)
\( \Rightarrow CD = DB = \frac{R}{2}\)
Do đó chu vi tứ giác \(ABDM\) là :
\(AB + BD + DM + MA = AB + DB + DC + CM + AM\) \( = 2R + \frac{R}{2} + \frac{R}{2} + 2R + 2R = 7R\)
c) Tia \(AC\) cắt tia \(By\) tại \(K.\) Chứng minh \(OK \bot BM.\)
\(\Delta AMO\) đồng dạng với \(\Delta BAK\) (\(\widehat {MAO} = \widehat {ABK} = 90^\circ ;\,\widehat {AOM} = \widehat {BKA}\) vì cùng phụ với \(\widehat {KAB}\))
Suy ra \(\frac{{AM}}{{AB}} = \frac{{AO}}{{BK}} \Rightarrow \frac{{AM}}{{AB}} = \frac{{BO}}{{BK}}\) \( \Rightarrow \tan \widehat {MBA} = \tan \widehat {OKB}\) \( \Rightarrow \widehat {MBA} = \widehat {OKB}\)
Gọi \(H\) là giao điểm của \(OK\) và \(BM\)
Ta có \(\widehat {MBA} = \widehat {OKB} \Rightarrow \widehat {HBO} = \widehat {OKB}\)
Mà \(\widehat {OKB} + \widehat {KOB} = 90^\circ \) (\(\Delta OBK\) vuông tại \(B\))
\( \Rightarrow \widehat {HBO} + \widehat {KOB} = 90^\circ \)
Hay \(\widehat {HBO} + \widehat {HOB} = 90^\circ \Rightarrow \widehat {OHB} = 90^\circ \)\( \Rightarrow OK \bot BM\) tại \(H.\)

