Một bình A hình trụ đứng, cách nhiệt, có diện tích đáy trong là S = 10
Câu hỏi
Nhận biếtMột bình A hình trụ đứng, cách nhiệt, có diện tích đáy trong là S = 100cm2 đặt trên mặt phẳng ngang. Bỏ vào bình A một khối trụ đứng B, làm bằng nhôm có diện tích đáy là S1 = 40cm2 chiều cao là h1, bên trong khối trụ B có một phần rỗng là chân không có thể tích V0. Sau đó đổ vào bình A một lít nước, khi có cân bằng, khối trụ nổi trong bình và chiều cao phần nổi là \(\frac{1}{4}{h_1}\), đáy dưới của khối trụ song song đáy bình và cách đáy trong của bình là x = 4cm (Hình 2).
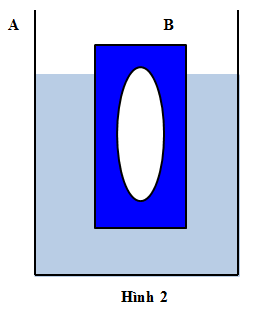
Biết khối lượng riêng của nước là D = 1000kg/m3, của nhôm là D1 = 2700kg/m3.
1) Tìm khối lượng m1 của trụ B, độ cao h1 và thể tích phần rỗng V0.
2) Khi cân bằng nhiệt thì nhiệt độ của nước và khối trụ B là t1 = 200C. Người ta đổ tiếp vào bình một lượng dầu có khối lượng m2, khối lượng D2 = 900kg/m3, nhiệt dung riêng c2,ở nhiệt độ t2 = 800C. Khi có cân bằng, đáy dưới khối trụ nằm ngay mặt phân cách giữa dầu và nước, khi đó nhiệt độ cân bằng của hệ là t = 300C. Biết nhiệt dung riêng của nước c = 4200 J/(kg.độ), của nhôm làm khối trụ B là c1 = 880J/(kg.độ).
Bỏ qua sự trao đổi nhiệt giữa hệ với không khí xung quanh và bình A.
Tìm m2 và c2.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: 1 lít = 1000 cm3
Chiều cao của nước trong bình trước khi thả vật là: \(H = \frac{V}{S} = 10cm\)
Vì lượng nước trong bình là không đổi nên:
\(\begin{array}{l}\frac{3}{4}{h_1}.\left( {S - {S_1}} \right) + x.S = H.S\\ \Rightarrow {h_1} = \left( {H - x} \right).\frac{S}{{S - {S_1}}}.\frac{4}{3} = 6.\frac{{100}}{{100 - 40}}.\frac{4}{3} = \frac{{40}}{3}cm\end{array}\)
Do khối trụ nổi nên:
\({P_{tru}} = {F_A} \Leftrightarrow 10.{m_1} = \frac{3}{4}{h_1}{S_1}.10D \Rightarrow {m_1} = \frac{3}{4}{h_1}{S_1}.D = 400g\)
Thể tích phần rỗng: \({V_0} = V - \frac{{{m_1}}}{{{D_1}}} = {h_1}{S_1} - \frac{{{m_1}}}{{{D_1}}} = \frac{{40}}{3}.40 - \frac{{400}}{{2,7}} = \frac{{10400}}{{27}}\left( {c{m^3}} \right) \approx 0,385\left( {lit} \right)\)
b) Giả sử vật chìm trong dầu đến độ cao h2 ta có:
\({m_2} = {h_2}{S_1}{D_2} \Rightarrow {h_2} = \frac{{100}}{9}cm < {h_1}\)
Khối lượng dầu đổ vào là:
\({m_2} = {D_2}{V_2} = {D_2}.{h_2}\left( {S - {S_1}} \right) = 0,9.\frac{{100}}{9}.60 = 600g\)
Xét phương trình trao đổi nhiệt:
\(\begin{array}{l}{Q_{toa}} = {Q_{thu}} \Leftrightarrow {m_2}{c_2}.\left( {{t_2} - t} \right) = \left( {mc + {m_1}{c_1}} \right)\left( {t - {t_1}} \right)\\ \Rightarrow {c_2} = \frac{{1.4200 + 0,4.880}}{{0,6}}.\frac{{30 - 20}}{{80 - 30}} = 1517,3\end{array}\)









