Lập phương trình chính tắc của hypebol (H) biết (H) có đỉnh A2(3;0) và đường tròn ngoại tiếp hình ch

Câu hỏi
Nhận biếtLập phương trình chính tắc của hypebol (H) biết (H) có đỉnh \({A_2}(3;0)\) và đường tròn ngoại tiếp hình chữ nhật cơ sở là: \((C):\,{x^2} + {y^2} = 16\).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
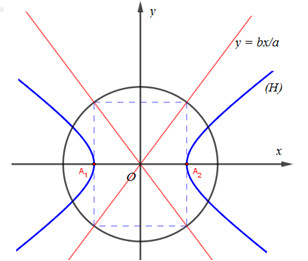
Gọi phương trình chính tắc của hypebol (H) là: \({{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1,\,\,(a,\,b > 0)\).
(H) có đỉnh \({A_2}(3;0) \Rightarrow a = 3\)
Đường tròn \((C):\,{x^2} + {y^2} = 16\) có bán kính \(R = 4\).
\( \Rightarrow {a^2} + {b^2} = {4^2} \Rightarrow c = 4\)
Mà \({a^2} + {b^2} = {c^2} \Rightarrow {3^2} + {b^2} = {4^2} \Leftrightarrow {b^2} = 7\)
Phương trình chính tắc của (H): \({{{x^2}} \over 9} - {{{y^2}} \over 7} = 1\).
Chọn: A
