Hình thang ABCD vuông ở A và B,;;AD = 2BC. Vẽ AH vuông góc BD,;;M là t

Câu hỏi
Nhận biếtHình thang \(ABCD\) vuông ở \(A\) và \(B,\;\;AD = 2BC.\) Vẽ \(AH \bot BD,\;\;M\) là trung điểm của \(DH.\) Chứng minh \(AM \bot MC.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
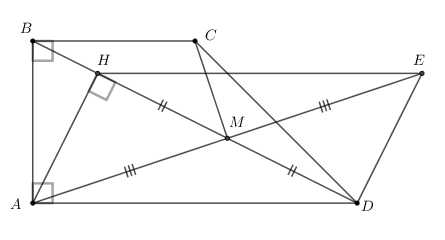
Lấy điểm \(E\) đối xứng với \(A\) qua \(M \Rightarrow AHED\) là hình bình hành (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường).
\( \Rightarrow \overrightarrow {HE} = \overrightarrow {AD} .\)
Khi đó ta có:
\(\begin{array}{l}\overrightarrow {AM} .\overrightarrow {CM} = \frac{1}{2}\overrightarrow {AE} .\left( {\overrightarrow {BM} - \overrightarrow {BC} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( {\overrightarrow {AH} + \overrightarrow {AD} } \right)\left( {2\overrightarrow {BM} - 2\overrightarrow {BC} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( {\overrightarrow {AH} + \overrightarrow {AD} } \right)\left( {2\overrightarrow {BM} - \overrightarrow {AD} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( {\overrightarrow {AH} .2\overrightarrow {BM} - \overrightarrow {AH} .\overrightarrow {AD} + \overrightarrow {AD} .2\overrightarrow {BM} - {{\overrightarrow {AD} }^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( {0 - \overrightarrow {AH} .\overrightarrow {AD} + 2\overrightarrow {AD} .\left( {\overrightarrow {AM} - \overrightarrow {AB} } \right) - A{D^2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( { - A{D^2} - \overrightarrow {AH} .\overrightarrow {AD} + 2\overrightarrow {AD} .\overrightarrow {AM} - 2\overrightarrow {AD} .\overrightarrow {AB} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( { - A{D^2} - \overrightarrow {AH} .\overrightarrow {AD} + \overrightarrow {AD} .\overrightarrow {AE} + 0} \right)\;\;\;\left( {do\;\;\overrightarrow {AE} = 2\overrightarrow {AM} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left[ { - A{D^2} - \overrightarrow {AD} \left( {\overrightarrow {AH} - \overrightarrow {AE} } \right)} \right]\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( { - A{D^2} - \overrightarrow {AD} .\overrightarrow {EH} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( { - A{D^2} + \overrightarrow {AD} .\overrightarrow {HE} } \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{1}{4}\left( { - A{D^2} + A{D^2}} \right) = 0.\\ \Rightarrow AM \bot CM\;\;\;\left( {dpcm} \right).\end{array}\)
