Hai bạn An và Bình đi dọc theo con đường thẳng AB và AC vuông góc nhau

Câu hỏi
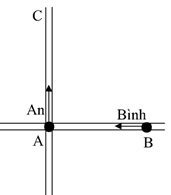
Nhận biếtHai bạn An và Bình đi dọc theo con đường thẳng AB và AC vuông góc nhau. An xuất phát từ A với vận tốc v1 = 2 m/s theo hướng AC. Cùng một lúc với An, Bình xuất phát từ B với vận tốc v2 = 1,5 m/s theo hướng BA ( hình vẽ). Sau thời gian t = 12s kể từ lúc đầu xuất phát. Coi hai bạn chuyển động đều.
a) Tính khoảng cách l giữa hai bạn lúc xuất phát.
b) Sau bao lâu kể từ lức xuất phát, khoảng cách giữa hai bạn gần nhau nhất ? Khoảng cách ấy bằng bao nhiêu?
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Quãng đường mỗi bạn đi là :
\({s_1} = {v_1}t;\,{s_2} = {v_2}t\)
Theo định lý Pi – ta – go ta có \({l^2} = s_1^2 + {\left( {l - {s_2}} \right)^2} = > l = {{v_1^2 + v_2^2} \over {2{v_2}}}t = 25m\)
b) Gọi d là khoảng cách giữa hai bạn sau thời gian t’
\(\eqalign{ & {d^2} = {\left( {{v_1}t'} \right)^2} + {\left( {25 - {v_2}t'} \right)^2} \cr & = > {d^2} = 6,25t{'^2} - 75t' + 625 \cr} \)
Khoảng cách d ngắn nhất khi t’= 6s
Khoảng cách ngắn nhất dmin = 20m









