Gọi N là giao điểm của AC và BD. Chứng minh MN vuông góc với AB.

Câu hỏi
Nhận biếtGọi N là giao điểm của AC và BD. Chứng minh MN vuông góc với AB.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
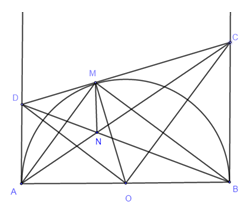
Gọi N là giao điểm của AC và BD. Chứng minh MN vuông góc với AB.
Ta có AD song song với BC
\( \Rightarrow \frac{{AD}}{{BC}} = \frac{{DN}}{{NB}}\) ( định lí Ta-lét trong tam giác)
Mà có: \(\left\{ \begin{array}{l}AD = DM\\BC = MC\end{array} \right.\left( {cmt} \right) \Rightarrow \frac{{DM}}{{MC}} = \frac{{DN}}{{NB}}\)
Xét tam giác BDC có: \(\frac{{DM}}{{MC}} = \frac{{DN}}{{NB}}\left( {cmt} \right)\)\( \Rightarrow MN//BC\) ( định lí Ta-lét đảo)
Mà có: \(BC \bot AB\) (do BC là tiếp tuyến với đường tròn)
Suy ra \(MN \bot AB\) (đpcm)\(\) \(\) \(\) \(\) \(\)

