Gọi I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH.
Câu hỏi
Nhận biếtGọi I là giao điểm của AD và CH. Chứng minh I là trung điểm của CH.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Có CH // BD=>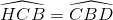 
(hai góc ở vị trí so le trong) mà ∆ BCD cân tại D
=> 
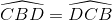nên CB là tia phân giác của 
.
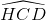do CA ┴ CB => CA là tia phân giác góc ngoài đỉnh C của ∆ ICD =>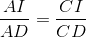 
(3)
Trong ∆ ABD có HI // BD =>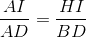 
(4).
Từ (3) và (4) =>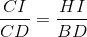 
mà CD = BD => CI = HI
=> I là trung điểm của CH
