[LỜI GIẢI] Giải và biện luận hệ bất phương trình : - Tự Học 365
KHỞI ĐỘNG CHO MÙA THI ĐẠI HỌC 2026

Ôn đúng trọng tâm – Học chắc từ hôm nay

BẮT ĐẦU NGAY

Giải và biện luận hệ bất phương trình :

Câu hỏi

Nhận biết

Giải và biện luận hệ bất phương trình :

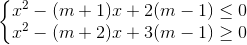
left{ egin{matrix} x^{2}-(m+1)x+2(m-1)leq 0 x^{2}-(m+2)x+3(m-1)geq 0 end{matrix}
ight." align="absmiddle" /> 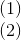egin{matrix} (1)(2) end{matrix}


Đáp án đúng:

Lời giải của Tự Học 365

Giải chi tiết:

Tam thức ở vế trái (1) có 2 nghiệm : x1 = m -1 ; x2 = 2

Tam thức ở vế trái (2) có 2 nghiệm : x3 = m – 1 ; x4 = 3

Ta xét 2 trường hợp ( phải so sánh 1 ; 2 ; m – 1 để lập bảng xét dấu):

+) m – 1 < 2 => m < 3

Ta có bảng xét dấu :

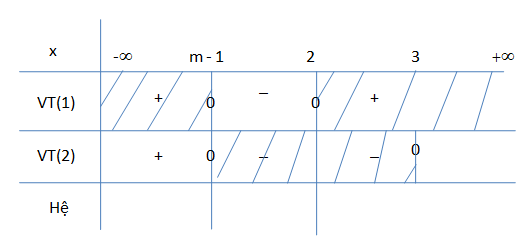
Nghiệm của hệ là x = m – 1  

+) m – 1 = 2 => m = 3, Hệ trở thành :

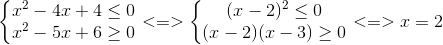
Vậy  x = 2

+) 2 < m -1 < 3 < => 3 < m < 4

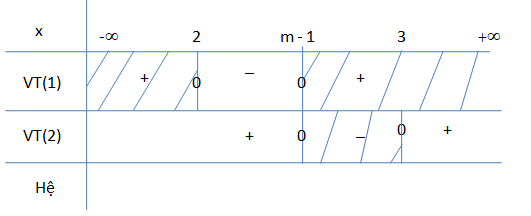
Nghiệm của hệ là [2 ; m -1]

+) m – 1 = 3  < => m =4 , Hệ trở thành :

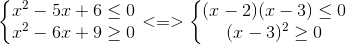
S = [2;3]

 

5) 3 < m – 1  < => m > 4

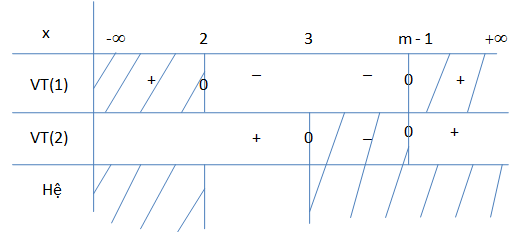
Nghiệm của hệ  là [2;3] v {m – 1}

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan

  • Giải Bất phương trình sau : 2x(3x-5) > 0

    Giải Bất phương trình sau :

    2x(3x-5) > 0

    Chi tiết
  • Khảo sát và vẽ đồ thị của hàm số :  1)y = 2|x| 2) y = 3√x

    Khảo sát và vẽ đồ thị của hàm số : 

    1)y = 2|x|

    2) y = 3√x

    Chi tiết
  • Định m sao cho : x<sup>2</sup> – (3m – 2)x + 2m<sup>2</sup>

    Định m sao cho : x2 – (3m – 2)x + 2m2 – 5m – 2 > 0 ; x ε R

    Chi tiết
  • Định m sao cho : mx<sup>2</sup> – 10x – 5 ≤ 0 ; x ε R  (1)

    Định m sao cho : mx2 – 10x – 5 ≤ 0 ; x ε R  (1)

    Chi tiết
  • TÌm a để 3 đường thẳng sau đây đồng qui: y=2x ; y= -x-3 ; y

    TÌm a để 3 đường thẳng sau đây đồng qui:

    y=2x ; y= -x-3 ; y= ax + 5

    Chi tiết
  • Định m để f(x) = x<sup>2</sup> – 2mx – m ≥ 0 với x > 0     

    Định m để f(x) = x2 – 2mx – m ≥ 0 với x > 0           

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx – 5 < 0 với x ε R   (1

    Định m để  f(x) = mx2 – mx – 5 < 0 với x ε R   (1)

    Chi tiết
  • Định m để  f(x) = mx<sup>2</sup> – mx + m + 3 ≥ 0 với x ε R 

    Định m để  f(x) = mx2 – mx + m + 3 ≥ 0 với x ε R 

    Chi tiết
  • Định m sao cho : (m+1)x<sup>2</sup> – 2(m+1)x + 4 > 0 ; x ε

    Định m sao cho : (m+1)x2 – 2(m+1)x + 4 > 0 ; x ε R  (1)

    Chi tiết
  • Định m để f(x) = mx<sup>2</sup> – 2(m+1)x – m + 5 > 0 với x

    Định m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x < 1

    Chi tiết