Giải và biện luận các bất phương trình : 1)
Câu hỏi
Nhận biếtGiải và biện luận các bất phương trình :
1) 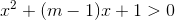 (1)
(1)
2) 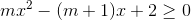 (2)
(2)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Ta có : ∆ = (m – 1)2 – 4 => ∆ = 0 < => m = -1 v m =3
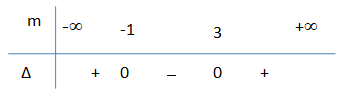
Ta xét các trường hợp :
+) – 1 < m < 3 < => ∆ < 0: thì VT (1) > 0 vì a = 1 > 0
+) m < -1 v 3 < m < => ∆ > 0: x2 + (m – 1)x + 1 = 0 có 2 nghiệm
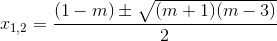
Ta có bảng xét dấu:
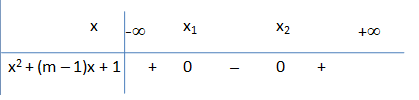
Do đó nghiệm của bất phương trình (1) là x < x1 và x2 < x
+) m = -1. Bất phương trình cho trở thành :
x2 – 2x + 1 > 0 < => (x+1)2 > 0 < => x ≠ -1
2) Ta xét 2 trường hợp :
+) m =0 thì (2) < => -x + 2 ≥ 0 < => x ≤ 2
+) m ≠ 0 thì ∆ = m2 – 6m + 1
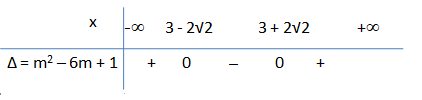
* m < 0 thì ∆ > 0 nên VT(2) = 0 có nghiệm
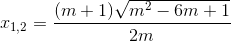
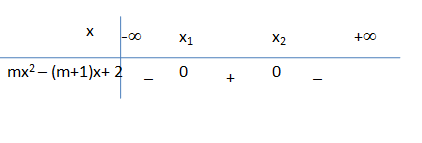
Vậy nghiệm của phương trình là : x1 ≤ x ≤ x2
* 0 < m < 3 - 2√2 hoặc m > 3 + 2√2 thì ∆ > 0
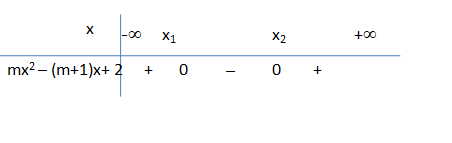
Vậy nghiệm của (2) là x ≤ x1 V x2 ≤ x và thỏa mãn 3 - 2√2 < m < 3 + 2√2 thì m > 0 và ∆ < 0
Bất phương trình (2) có nghiệm tùy ý S = R
* Khi m = 3 ± 2√2 => ∆ = 0 , Bất phương trình có nghiệm tùy ý.

