Giả sử x y z là những số thực dương thỏa mãn điều kiện : x + y + z = 1 Chứng minh rằng: <
Câu hỏi
Nhận biếtGiả sử x, y, z là những số thực dương thỏa mãn điều kiện : x + y + z = 1
Chứng minh rằng: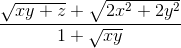 
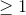
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Có 
≤ (z + x)(z + y) = z2 + zx + zy +xy = z(x + y + z) + xy = z + xy
Suy ra 
≥ 
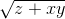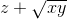(1)
Ta có
2x2 + 2y2 ≥ (x + y)2 =>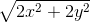 
≥ x + y (2)
Cộng hai bất đẳng thức (1) và (2) ta thu được:
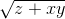≥ x + y + z + 
= 1 +
Suy ra 
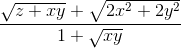≥ 1.
Dấu đẳng thức xảy ra <=>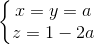 
(0 < a < 
)
