Giả sử KE = KC. Chứng minh: OK // MN và KM2 + KN2 = 4R2
Câu hỏi
Nhận biếtGiả sử KE = KC. Chứng minh: OK // MN và KM2 + KN2 = 4R2
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: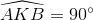 
=> 
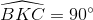=> ∆ KEC vuông tại K.
Theo giả thiết ta lại có: KE = KC nên tam giác KEC vuông cân tại K
=> 
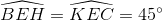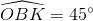
Mặt khác, vì ∆ OBK cân tại O (do OB = OK = R) nên suy ra ∆ OBK vuông cân tại O dẫn đến OK // MN (cùng vuông góc với AB).
Gọi P là giao điểm của tia KO với đường tròn thì ta có KP là đường kính và KP // MN. Ta có tứ giác KPMN là hình thang cân nên KN = MP
Xét ∆ KMP vuông ở M ta có:
MP2 + MK2 = KP2 <=> KM2 + KN2 = 4R2
