. Đường thẳng ( d )thay đổi đi qua M, không đi qua O, và luôn cắt đườn

Câu hỏi
Nhận biếtCho đường tròn tâm O và điểm M nằm ngoài đường tròn đó. Qua M kẻ các tiếp tuyến \(MA;\,MB\) với đường tròn (\(A,\,B\) là tiếp điểm). Đường thẳng \(\left( d \right)\)thay đổi đi qua M, không đi qua O, và luôn cắt đường tròn tại hai điểm phân biệt \(C\) và \(D\) (C nằm giữa \(M\) và \(D\))
a) Chứng minh \(AMBO\) là tứ giác nội tiếp.
b) Chứng minh \(MC.MD = M{A^2}.\)
c) Chứng minh đường tròn ngoại tiếp \(\Delta OCD\) luôn đi qua điểm cố định khác \(O.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
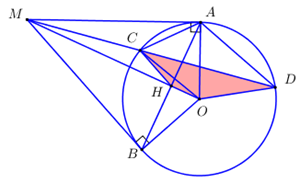
a) Chứng minh \(AMBO\) là tứ giác nội tiếp
Do \(MA,\,\,MB\) là các tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A,\,\,B\) nên \(\angle OAM = \angle OBM = {90^0}\).
Xét tứ giác \(AMBO\) có: \(\angle OAM + \angle OBM = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(AMBO\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh \(MC.MD = M{A^2}\).
Xét tam giác \(MCA\) và tam giác \(MAD\) có:
\(\angle AMD\) chung;
\(\angle MAC = \angle MDA\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(AC\));
\( \Rightarrow \Delta MCA \sim \Delta MAD\,\,\left( {g.g} \right) \Rightarrow \frac{{MC}}{{MA}} = \frac{{MA}}{{MD}} \Rightarrow MC.MD = M{A^2}\) (1).
c) Chứng minh đường tròn ngoại tiếp tam giác \(OCD\) luôn đi qua điểm cố định khác \(O\).
Gọi \(H = OM \cap AB\,\,\left( {H \ne O} \right)\).
Ta có \(OA = OB\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của \(AB\).
\(MA = MB\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow M\) thuộc trung trực của \(AB\).
\( \Rightarrow OM\) là trung trực của \(AB\) \( \Rightarrow OM \bot AB\) tại \(H\).
Áp dụng hệ thức lượng trong tam giác vuông \(OAM\) ta có: \(M{A^2} = MH.MO\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow MC.MD = MH.MO \Rightarrow \frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\).
Xét tam giác \(MCH\) và tam giác \(MOD\) có :
\(\angle OMD\) chung;
\(\frac{{MC}}{{MH}} = \frac{{MO}}{{MD}}\,\,\left( {cmt} \right)\);
\( \Rightarrow \Delta MCH \sim \Delta MOD\,\,\left( {c.g.c} \right) \Rightarrow \angle MHC = \angle MDO = \angle CDO\) (hai góc tương ứng).
Mà \(\angle MHC + \angle OHC = {180^0}\) (kề bù) \( \Rightarrow \angle CDO + \angle OHC = {180^0} \Rightarrow \) Tứ giác \(OHCD\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
\( \Rightarrow H\) thuộc đường tròn ngoại tiếp tam giác \(OCD\).
Mà \(O,\,\,M\) cố định \( \Rightarrow A,\,\,B\) cố định \( \Rightarrow H = OM \cap AB\) cố định.
Vậy đường tròn ngoại tiếp tam giác \(OCD\) luôn đi qua điểm \(H = OM \cap AB\,\,\left( {H \ne O} \right)\) cố định (đpcm).

