đường kính AB. Trên đường thẳng AB lấy điểm C sao cho B nằm giữa A,C.
Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) đường kính \(AB\). Trên đường thẳng \(AB\) lấy điểm \(C\) sao cho \(B\) nằm giữa \(A,C\). Kẻ tiếp tuyến \(CK\) với đường tròn \(\left( O \right)\,\,(K\) là tiếp điểm), tiếp tuyến tại \(A\) của đường tròn \(\left( O \right)\) cắt đường thẳng \(CK\) tại \(H\). Gọi \(I\) là giao điểm của \(OH\) và \(AK,\,\,\,J\) là giao điểm của \(BH\) với đường tròn \(\left( O \right)\,\,(J\) không trùng với \(B\)).
a) Chứng minh \(AJ.HB = AH.AB\).
b) Chứng minh 4 điểm \(B,\,\,O,\,\,I,\,\,J\) cùng nằm trên một đường tròn.
c) Đường thẳng vuông góc với \(AB\) tại \(O\) cắt \(CH\) tại \(P\). Tính \(\frac{{AH}}{{HP}} - \frac{{HP}}{{CP}}\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
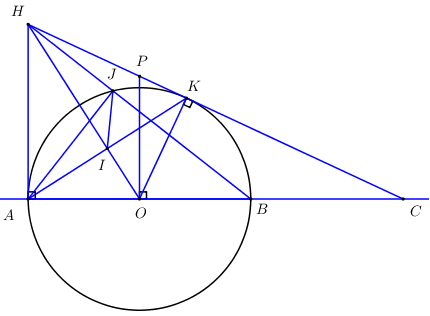
a) Chứng minh \(AJ.HB = AH.AB\).
Ta có \(\angle AJB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AJ \bot BJ \Rightarrow AJ \bot BH\);
\(AH\) là tiếp tuyến của \(\left( O \right)\) tại \(A \Rightarrow AH \bot AB \Rightarrow \angle HAB = {90^0}\).
Xét tam giác \(ABJ\) và tam giác \(HBA\) có:
\(\begin{array}{l}\angle AJB = \angle HAB = {90^0};\\\angle ABH\,\,chung;\\ \Rightarrow \Delta ABJ \sim \Delta HBA \Leftrightarrow \frac{{AJ}}{{AH}} = \frac{{AB}}{{HB}}\,\,\left( {g.g} \right) \Leftrightarrow AJ.HB = AH.AB\,\,\,\left( {dpcm} \right).\end{array}\)
b) Chứng minh 4 điểm \(B,\,\,O,\,\,I,\,\,J\) cùng nằm trên một đường tròn.
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có \(HA = HK \Rightarrow H\) thuộc trung trực của \(AK\) .
Lại có \(OA = OK\,\,\left( { = R} \right) \Rightarrow O\) thuộc trung trực của \(AK\).
Suy ra \(OH\) là trung trực của \(AK \Rightarrow OH \bot AK\) tại \(I \Rightarrow \angle AIH = {90^0}\).
Xét tứ giác \(AIJH\) có: \(\angle AIH = \angle AJH = {90^0}\).
\( \Rightarrow \) Tứ giác \(AIJH\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle JIH = \angle JAH\) (2 góc nội tiếp cùng chắn cung \(JH\)).
Mà \(\angle JAH = \angle JBA\) (cùng phụ với \(\angle JAB\));
\( \Rightarrow \angle JIH = \angle JBA = \angle JBO \Rightarrow \) Tứ giác \(OIJB\) là tứ giác nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện) hay 4 điểm \(B,\,\,O,\,\,I,\,\,J\) cùng nằm trên một đường tròn.
c) Đường thẳng vuông góc với \(AB\) tại cắt \(CH\) tại \(P\). Tính \(\frac{{AH}}{{HP}} - \frac{{HP}}{{CP}}\).
Áp dụng tính chất 2 tiếp tuyến cắt nhau có: \(\angle AHO = \angle OHP\).
Có: \(\left\{ \begin{array}{l}OP \bot AB\\AH \bot AB\end{array} \right.\,\,\left( {gt} \right) \Rightarrow OP//AH \Rightarrow \angle AHO = \angle POH\) (so le trong)
\( \Rightarrow \angle OHP = \angle POH \Rightarrow \Delta POH\) cân tại \(P \Rightarrow OP = HP\) (tính chất tam giác cân).
Áp dụng định lí Ta-lét ta có: \(\frac{{AH}}{{HP}} = \frac{{AH}}{{OP}} = \frac{{AC}}{{OC}};\,\,\frac{{HP}}{{CP}} = \frac{{AO}}{{OC}}\)
\( \Rightarrow \frac{{AH}}{{HP}} - \frac{{HP}}{{CP}} = \frac{{AC}}{{OC}} - \frac{{AO}}{{OC}} = \frac{{OC}}{{OC}} = 1\).
Vậy \(\frac{{AH}}{{HP}} - \frac{{HP}}{{CP}} = 1\,\).
