Định m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x
Câu hỏi
Nhận biếtĐịnh m để f(x) = mx2 – 2(m+1)x – m + 5 > 0 với x < 1
Đáp án đúng: C
Lời giải của Tự Học 365
Lời giải chi tiết:
+) TH1 : m = 0 thì f(x) = 5 – 2x > 0 < => x < 5/2 Thỏa mãn
=> Nhận m = 0
+) TH2 : m ≠ 0
a) m > 0
* f(x) > 0 với x > 1 < => ∆’ = 2m2 – 3m – 1 < 0 < => ½ < m < 1 ( thỏa mãn m > 0 )
* Nếu ∆’ ≥ 0 ta có bảng xét dấu :
Nên f(x) > 0 với x < 1 < => 1 ≤ x1 ≤ x2
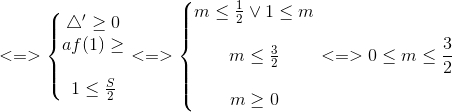b) m < 0
* Nếu ∆ < 0 => f(x) < 0 với mọi x không thỏa mãn đề bài
* Nếu ∆’ ≥ 0 ta có bảng xét dấu :
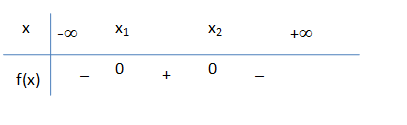
Thì f(x) > 0 với mọi x < 0 cũng vô nghiệm
Tóm lại 0 ≤ m ≤ 3/2
Chọn C