Điện tích q = 10-8 C di chuyển dọc theo các cạnh của tam giác

Câu hỏi
Nhận biếtĐiện tích q = 10-8 C di chuyển dọc theo các cạnh của tam giác đều ABC cạnh a = 10 cm trong điện trường đều cường độ điện trường là E = 300 V/m, \( \overrightarrow E //BC \). Tính công của lực điện trường khi q di chuyển trên mỗi cạnh của tam giác:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Cách giải:
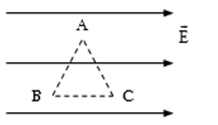
Công của lực điện trường khi q di chuyển trên cạnh AB là:
\({A_{AB}}\; = q.E.AB.cos{120^0} = {10^{ - 8}}.300.0,1.\left( { - 0,5} \right){\rm{ }} = - 1,{5.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh BC là:
\({A_{BC}}\; = q.E.BC = {10^{ - 8}}.300.0,1 = {3.10^{ - 7}}\;J\)
Công của lực điện trường khi q di chuyển trên cạnh AC là:
\({A_{AC}}\; = q.E.AC.cos60 = {10^{ - 8}}.300.0,1.0,5 = 1,{5.10^{ - 7}}\;J\)
Chọn C
Luyện tập
Câu hỏi liên quan
-





Đặt một hiệu điện thế U không đổi vào hai cực của bình điện phân. Xét trong cùng một khoảng thời gian, nếu kéo hai cực của bình ra xa sao cho khoảng cách giữa chúng tăng gấp 2 lần thì khối lượng chất được giải phóng ở điện cực so với lúc trước sẽ:



