Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray

Câu hỏi
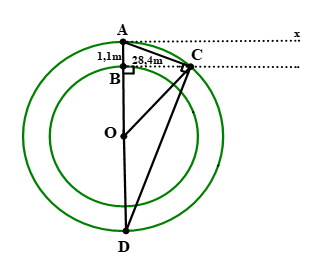
Nhận biếtĐể giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình bên). Biết chiều rộng của đường ray là AB ≈1,1m, đoạn BC ≈28,4m. Hãy tính bán kính OA = R của đoạn đường ray hình vòng cung?
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Thanh ray trùng với BC tiếp xúc với đường tròn (O, OB) tại B nên là tiếp tuyến của đường tròn (O, OB)
\(\Rightarrow BC\bot OB\)
OA cắt đường tròn (O, OA) tại điểm D \(\left( D\ne A \right)\) \(\Rightarrow AD=2R\) Tam giác ACD nội tiếp đường tròn (O, OA) có đường kính AD nên là tam giác vuông tại C. Xét tam giác ACD vuông tại C, đường cao BC, ta có:
\(C{{B}^{2}}=AB.BD\) (hệ thức lượng trong tam giác vuông)
\(\begin{array}{l} \Leftrightarrow C{B^2} = AB.\left( {AD - AB} \right)\\ \Leftrightarrow C{B^2} = AB.\left( {2R - AB} \right)\end{array}\)
Thay số, ta có:
\(\begin{array}{l}{\left( {28,4} \right)^2} \approx 1,1.\left( {2R - 1,1} \right)\\ \Leftrightarrow 2R \approx 807,77\\ \Leftrightarrow R \approx 367,2m\end{array}\)