Cùng một thời điểm, một chiếc ô tô XA xuất phát từ thành phố A hướng v
Câu hỏi
Nhận biếtCùng một thời điểm, một chiếc ô tô XA xuất phát từ thành phố A hướng về thành phố B và một chiếc ô tô khác XB xuất phát từ thành phố B hướng về thành phố A. Chúng chuyển động với vận tốc riêng không đổi và gặp nhau lần đầu tiên tại một điểm cách A 20 km. Cả hai chiếc xe sau khi đến B và A tương ứng, lập tức quay trở lại và chúng gặp nhau lần thứ hai tại một điểm C. Biết thời gian xe XB đi từ C đến B là 10 phút và thời gian giữa hai lần gặp nhau là 1 giờ. Hãy tính vận tốc của từng chiếc ô tô.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Gọi x, y lần lượt là vận tốc của ô tô XA và XB ; x, y tính bằng km/h và x > 0; y > 0
Độ dài quãng đường CB là:
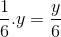(đổi 10' = 
giờ)
Một giờ ô tô XA đi được:
1.x = MC + CB + CB => x = MC +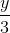 
=> MC = x -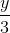
Một giờ ô tô XB đi được :
1.y = 20 + 20 + MC => y = 40 + MC => MC = y - 40.
Ta có phương trình: x - 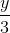= y - 40
Thời gian hai ô tô đã đi để gặp nhau lần thứ nhất là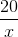 
, nên ta có phương trình:
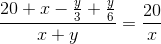
Vậy ta có hệ phương trình sau:
<=> 
<=> 
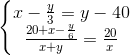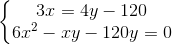
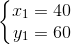và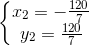 
(bị loại vì x < 0).
Nghiệm thứ nhất (x; y) =(40; 60) thỏa mãn điều kiện bài toán. Vậy vận tốc của xe XA = 40 km/h và XB = 60 km/h
