Có hai vật nhỏ M1 và M2, ban đầu cách nhau một khoảng AB = a.

Câu hỏi
Nhận biếtCó hai vật nhỏ M1 và M2, ban đầu cách nhau một khoảng AB = a. Cùng lúc hai vật chuyển động thẳng đều, M2 chuyển động theo đường thẳng AB về phía B với vận tốc v1 = 2v, M2 chuyển động đều theo đường thẳng BC về phía C với vận tốc v2 = v. Tìm khoảng cách giữa nhỏ nhất giữa hai vật và khoảng thời gian từ lúc hai vật bắt đầu chuyển động đến khi khoảng cách giữa hai vật nhỏ nhất. Biết rằng AB hợp với BC một góc ( 0 < < 900) như hình 1.
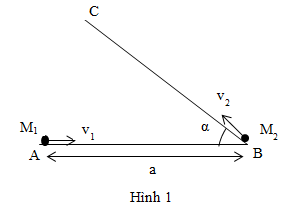
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Chọn gốc toạ độ tại A. Hệ quy chiếu như hình vẽ.
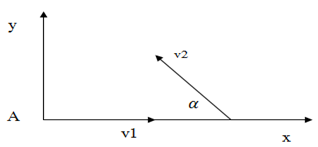
Vật 1:
\(\left\{ \matrix{ {x_1} = {v_1}t \hfill \cr {y_1} = 0 \hfill \cr} \right.\)
Vật 2:
\(\left\{ \matrix{ {x_2} = a - {v_2}c{\rm{os}}\alpha t \hfill \cr {y_1} = {v_2}\sin \alpha t \hfill \cr} \right.\)
Khoảng cách hai vật M1 và M2: \({d_{12}} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \)
Đặt \(f(t) = {\left( {{x_2} - {x_1}} \right)^2} + {\left( {{y_2} - {y_1}} \right)^2}\)
d12min khi f (t)min
Ta có: \(f(t) = {\left[ {a - \left( {{v_1} + {v_2}c{\rm{os}}\alpha } \right)t} \right]^2} + {({v_2}\sin \alpha t)^2} = \left( {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha } \right){t^2} - 2a({v_1} + {v_2}c{\rm{os}}\alpha )t + {a^2}\)
f(t) là phương trình bậc hai có hệ số lớn hơn 0
Suy ra: \(f{(t)_{\min }} = {{{{\left[ {2a({v_1} + {v_2}c{\rm{os}}\alpha )} \right]}^2} - 4{a^2}\left( {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha } \right)} \over {4\left( {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha } \right)}} = {{{a^2}{v_2}^2 - {a^2}{v_2}^2c{\rm{o}}{{\rm{s}}^2}\alpha } \over {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha }}\)
Khi \(t = {{2a({v_1} + {v_2}c{\rm{os}}\alpha )} \over {2\left( {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha } \right)}} = {{a({v_1} + {v_2}c{\rm{os}}\alpha )} \over {\left( {{v_1}^2 + {v_2}^2 + 2{v_1}{v_2}c{\rm{os}}\alpha } \right)}}\)
Thay v1 = 2v; v2 = v ta được:
\(\left\{ \matrix{ f{(t)_{\min }} = {{{a^2}{{\sin }^2}\alpha } \over {5 + 4c{\rm{os}}\alpha }} \hfill \cr t = {{a(2 + c{\rm{os}}\alpha )} \over {5v + 4v\cos \alpha }} \hfill \cr} \right. \to \left\{ \matrix{ {d_{12\min }} = \sqrt {f{{(t)}_{\min }}} = \sqrt {{{{a^2}{{\sin }^2}\alpha } \over {5 + 4c{\rm{os}}\alpha }}} \hfill \cr t = {{a(2 + c{\rm{os}}\alpha )} \over {5v + 4v\cos \alpha }} \hfill \cr} \right.\)









