Chứng minh tam giác MBN là tam giác đều.
Câu hỏi
Nhận biếtChứng minh tam giác MBN là tam giác đều.
Đáp án đúng: A
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
AB vuông góc với MN (giả thiết)
=> C là trung điểm của MN
=> AB là trung trực của MN nên BM=BN hay tam giác BMN cân tại B.
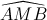= 900(góc nội tiếp chắn nửa đường tròn ). Xét tam giác vuông AMB có CM là đường cao nên:
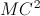= AC.CB = 
.
= 
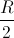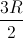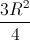=> MC = 
.
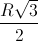BC=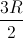 => tan 
= 
= : = 
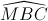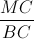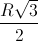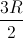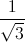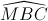=> = 300
=> 
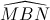=600 .Do đó tam giác BMN là tam giác đều.
