Chứng minh tam giác AMN vuông cân.

Câu hỏi
Nhận biếtChứng minh tam giác \(AMN\) vuông cân.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
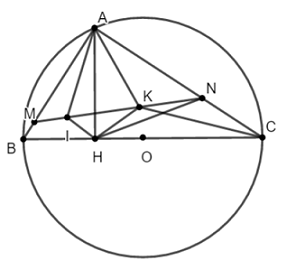
Ta có: \(\angle BAH = \angle ACH\)(cùng phụ với \(\angle ABH\)).
\( \Rightarrow \angle IAH = \angle HCK\)( tính chất phân giác)
Mà \(\angle IHA = \angle KHC\,\,\,\left( { = {{45}^0}} \right)\)
Suy ra \(\Delta HIA\)đồng dạng với \(\Delta HKC\) (g.g).
\( \Rightarrow \dfrac{{HI}}{{HK}} = \dfrac{{HA}}{{HC}}\)\( \Rightarrow \dfrac{{HI}}{{HA}} = \dfrac{{HK}}{{HC}}\)
Mà \(\angle IHK = {90^0}\) (góc tạo bởi hai đường phân giác của hai góc kề bù).
\(\angle AHC = {90^0}\,\,\left( {gt} \right)\).
Suy ra \(\Delta IHK\)đồng dạng với \(\Delta AHC\) (c.g.c) \( \Rightarrow \)\(\angle IKH = \angle ACH\)(hai góc tương ứng).
\( \Rightarrow HKNC\)là tứ giác nội tiếp (tứ giác có góc ngoài và góc trong tại đỉnh đổi diện bằng nhau).
\( \Rightarrow \angle ANM = \angle KHC = {45^0}\)(Góc ngoài và góc trong tại đỉnh đổi diện bằng nhau)
Vậy \(\Delta ANM\) vuông cân tại \(A\) (Tam giác vuông có 1 góc bằng \({45^0}\)).

