Chứng minh rằng (P) và (d) cắt nhau tại hai điểm phân biệt với mọi m. Gọi y1 ; y2 là các tung độ g

Câu hỏi
Nhận biếtChứng minh rằng (P) và (d) cắt nhau tại hai điểm phân biệt với mọi m.
Gọi y1 ; y2 là các tung độ giao điểm của (P) và (d), tìm m để y1 + y2 < 9
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Phương trình hoành độ giao điểm của Parabol (P): y = x2 và đường thẳng (d): y = 2mx – 2m + 3 là :
X2 = 2mx -2m + 3 <=> x2 – 2mx + 2m – 3 = 0 (*)
Ta có: ∆’ = m2 – 2m + 3 = (m – 1)2 + 2 > 0 với mọi giá trị m nên (*) luôn có hai nghiệm phân biệt hay (P) cắt (d) tại hai điểm phân biệt với mọi m.
Gọi tọa độ giao điểm của (P) và (d) là (x1; y1); (x2; y2) ta có x1; x2 là nghiệm của (*) nên:
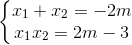 và
và 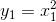 ;
; 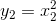
Suy ra:
y1 + y2 < 9 <=> x12 + x22 < 9 <=> (x1 + x2)2 – 2x1x2 < 9
<=> 4m2 – 4m + 6 < 9 <=> (2m – 1)2 < 4 <=> -2 < 2m – 1 < 2
<=>  < m <
< m < 

