Chứng minh rằng 2HD.AB = DA.BC.

Câu hỏi
Nhận biếtChứng minh rằng \(2HD.AB = DA.BC\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
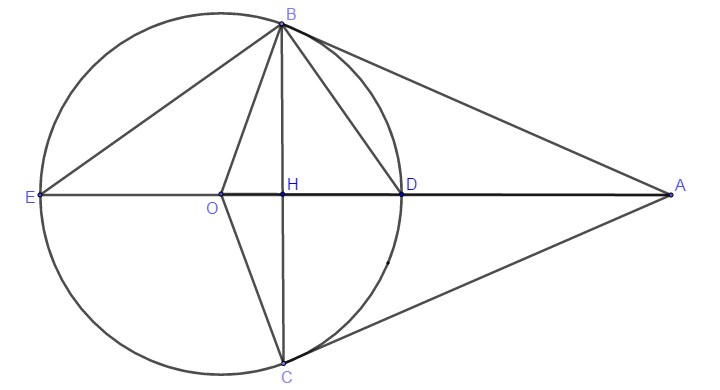
Có D nằm trên đường trung trực của BC (D nằm trên OA)
Suy ra \(BD = BC\) (tính chất đường trung trực), suy ra cung BD bằng cung DC (hai cung bằng nhau thì căng hai dây bằng nhau)
Xet đường tròn \(\left( {O;R} \right)\)có:
+) \(\angle CBD\) là góc nội tiếp chắn cung DC
+) \(\angle DBA\) là góc tạo bởi tiếp tuyến và dây cung chắn cung BD
+) Cung BD và cung DC bằng nhau (cmt)
\( \Rightarrow \angle CBD = \angle DBA \Rightarrow BD\)là phân giác \(\angle HBA\)
Áp dụng tính chất đường phân giác vào tam giác HBA có: \(\frac{{HD}}{{DA}} = \frac{{BH}}{{AB}} \Rightarrow HD.AB = DA.BH\)
Mà có: \(BH = \frac{1}{2}BC\) (do H là trung điểm của BC)
\( \Rightarrow HD.AB = DA.\frac{{BC}}{2} \Leftrightarrow 2HD.AB = DA.BC\) (đpcm)

