Chứng minh phương trình (1) luôn có không quá hai nghiệm phân biệt.

Câu hỏi
Nhận biếtChứng minh phương trình (1) luôn có không quá hai nghiệm phân biệt.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
(1) ⇔ 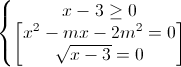
⇔ 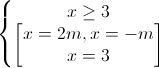
Nếu m ≥ 0 thì x = 2m ≥ 0, x = - m ≤ 0
Nếu m ≤ 0 thì x = 2m ≤ 0, x = - m ≥ 0
Do vậy phương trình x2 – mx – 2m2 = 0 có nhiều nhất một nghiệm lớn hơn hoặc bằng 3.
Như vậy, phương trình (1) luôn có không quá hai nghiệm phân biệt.

