Chứng minh BC vuông góc với OA và BA.BE = AE.BO.
Câu hỏi
Nhận biếtChứng minh BC vuông góc với OA và BA.BE = AE.BO.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
AB, AC là các tiếp tuyến của đường tròn (O) (gt)
=>AB = AC, AO là tia phân giác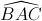 
(tính chất của hai tiếp tuyến cắt nhau)
∆ABC cân tại A, AO là đường phân giác nên AO cũng là đường cao của ∆ABC
=> BC ⊥OA
Xét ∆EAB và ∆EBO có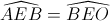 
( = 900);
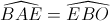(cùng phụ với 
)
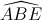Do đó ∆EAB ~ ∆EBO (g.g) =>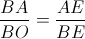 
Vậy BA.BE = AE.BO
