Chứng minh BC là tia phân giác của <
Câu hỏi
Nhận biếtChứng minh BC là tia phân giác của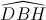 
và tứ giác BDCH là hình thoi.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có ∆ABC cân tại A (gt), AI là đường cao nên AI là tia phân giác của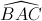 
=> 
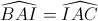
Mà 
(hệ quả góc tạo bởi tia tiếp tuyến và dây cung)
(hai góc nội tiếp chắn cung KI)
Do đó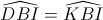 
Vậy BC là tia phân giác của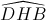 
∆BHD có BI là đường phân giác và là đường cao nên ∆BHD cân tại B => BI là đường trung tuyến => IH = ID
Tứ giác BDCH có I là trung điểm của BC, HD nên tứ giác BDCH là hình bình hành.
Mà HD⊥BC.
Vậy tứ giác BHCD là hình thoi.
