Cho x y là các số thực dương thỏa mãn điều kiện xy ≤ 1. Chứng minh rằng <
Câu hỏi
Nhận biếtCho x, y là các số thực dương thỏa mãn điều kiện xy ≤ 1. Chứng minh rằng 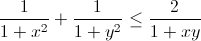. Dấu bằng xảy ra khi và chỉ khi nào?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
⇔ 
⇔ 
⇔ 
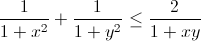
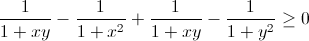
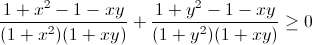
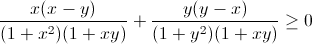
⇔ x(x – y)(1 + y2) + y(y – x)(1 + x2) ≥ 0
⇔ (x – y)[x(1 + y2) – y(1 + x2)] ≥ 0
⇔(x – y)[x(1 + y2) – y(1 + x2)] ≥ 0
⇔(x – y)(x + xy2 – y – x2y) ≥ 0
⇔ (x – y)[(x – y) – xy(x – y)] ≥ 0
⇔ (x – y)2(1 – xy) ≥ 0
(Bất đẳng thức , vì (x – y)2 ≥ 0 và xy ≤ 1 ⇔ 1 – xy ≥ 0)
Dấu “=” xảy ra khi và chỉ khi x = y hoặc xy = 1.
